密码学 数字签名

数字签名是消息认证的公钥基本原理。在现实世界中，在手写或打印的消息上使用手写签名很常见。它们用于将签名者绑定到消息。

类似地，数字签名是一种将个人/实体绑定到数字数据的方法。这种绑定可以由接收方以及任何第三方独立验证。

数字签名是从数据和仅签名者知道的密钥计算出的加密值。

在现实世界中，消息接收者需要确保消息属于发送者，并且发送者不应该能够否认该消息的来源。此要求在业务应用程序中非常关键，因为交换数据发生争议的可能性非常高。

数字签名模型

如前所述，数字签名方案基于公钥密码学。数字签名方案的模型如下图所示：

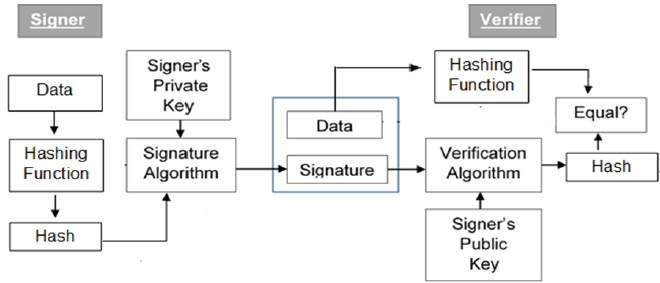
以下几点详细解释了整个过程：

• 每个采用此方案的人都有一个公钥-私钥对。

• 通常，用于加密/解密和签名/验证的密钥对是不同的。用于签名的私钥称为签名密钥，公钥称为验证密钥。

• 签名者将数据馈送到哈希函数并生成数据的哈希值。

• 然后将哈希值和签名密钥馈送到签名算法，该算法生成给定哈希值的数字签名。签名附加到数据，然后两者都发送到验证者。

• 验证者将数字签名和验证密钥输入到验证算法中。验证算法输出一些值。

• 验证者还对接收到的数据运行相同的哈希函数以生成哈希值。

• 为了验证，将此哈希值与验证算法的输出进行比较。根据比较结果，验证者确定数字签名是否有效。

• 由于数字签名是由签名者的“私钥”创建的，并且任何人都无法拥有此密钥；签名者将来无法否认签署数据。

需要注意的是，签名算法通常不是直接对数据进行签名，而是创建数据的哈希值。由于数据哈希是数据的唯一表示，因此对哈希值进行签名足以代替对数据进行签名。使用哈希而不是直接对数据进行签名的最重要的原因是方案的效率。

假设 RSA 用作签名算法。如公钥加密章节所述，使用 RSA 的加密/签名过程涉及模幂运算。

通过模幂运算对大型数据进行签名在计算上代价高昂且耗时。数据的哈希值是数据的相对较小的摘要，因此对哈希值进行签名比对整个数据进行签名更有效。

数字签名的重要性

在所有加密基本原理中，使用公钥密码学的数字签名被认为是实现信息安全非常重要和有用的工具。

除了能够提供消息不可否认性之外，数字签名还提供消息认证和数据完整性。让我们简要了解一下数字签名是如何实现这一点的：

• 消息认证 - 当验证者使用发送者的公钥验证数字签名时，他确信签名仅由拥有相应私钥的发送者创建，而不是其他人。

• 数据完整性 - 如果攻击者可以访问数据并对其进行修改，则接收端处的数字签名验证将失败。修改后的数据的哈希值和验证算法提供的输出将不匹配。因此，接收者可以安全地拒绝该消息，假设数据完整性已被破坏。

• 不可否认性 - 由于假设只有签名者知道签名密钥，因此他只能在给定数据上创建唯一的签名。因此，如果将来发生任何争议，接收者可以向第三方出示数据和数字签名作为证据。

通过将公钥加密添加到数字签名方案中，我们可以创建一个可以提供安全性的四个基本要素的密码系统，即：隐私、身份验证、完整性和不可否认性。

带数字签名的加密

在许多数字通信中，希望交换加密消息而不是明文以实现机密性。在公钥加密方案中，发送者的公钥（加密密钥）在开放域中可用，因此任何人都可以伪造其身份并将任何加密消息发送到接收者。

这使得使用 PKC 进行加密的用户必须寻求数字签名以及加密数据，以确保消息认证和不可否认性。

这可以通过将数字签名与加密方案相结合来实现。让我们简要讨论一下如何实现此要求。有两种可能性，先签名后加密和先加密后签名。

但是，基于先签名后加密的密码系统可能会被接收者利用来伪造发送者的身份并将该数据发送到第三方。因此，此方法不受欢迎。先加密后签名的方法更可靠且被广泛采用。这在下图中进行了说明：

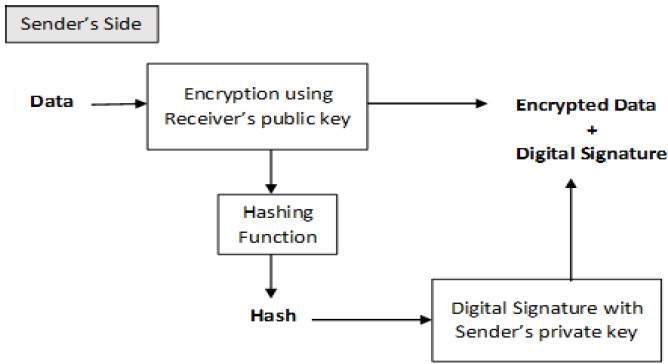
接收者在收到加密数据和签名后，首先使用发送者的公钥验证签名。在确保签名的有效性后，他然后使用自己的私钥通过解密检索数据。