密码学 - Feistel分组密码

上一页
下一页

Feistel 密码是一种框架或设计模型，用于创建不同的对称分组密码，包括 DES。此设计框架的组件可以是自反的、不可反的或可反的。加密和解密算法与 Feistel 分组密码使用的算法相同。

Feistel 结构演示了混淆和扩散的实现过程，并且基于 1945 年首次描述的 Shannon 结构。使用替换方法，混淆在加密密钥和密文之间创建复杂的关系。但是扩散使用置换过程来创建明文和密文之间的复杂链接。

Feistel 密码提出了交替实现替换和置换的框架。替换使用密文代替明文元素。置换不是像替换那样用一个元素替换另一个元素，而是重新排列明文的元素。

算法

  • 列出明文中的每个字符。

  • 将明文转换为 ASCII 后，将其格式化为 8 位二进制。

  • 将二进制明文字符串分成左右两部分 (L1 和 R1)。

  • 对于每一轮，生成两个随机二进制密钥 (K1 和 K2)，每个密钥的长度都与明文相同。

加密

在 Feistel 密码加密过程中，明文会经过多轮处理。每一轮都包含替换步骤和置换步骤。请查看下面的示例，该示例描述了此设计框架中使用的加密结构。

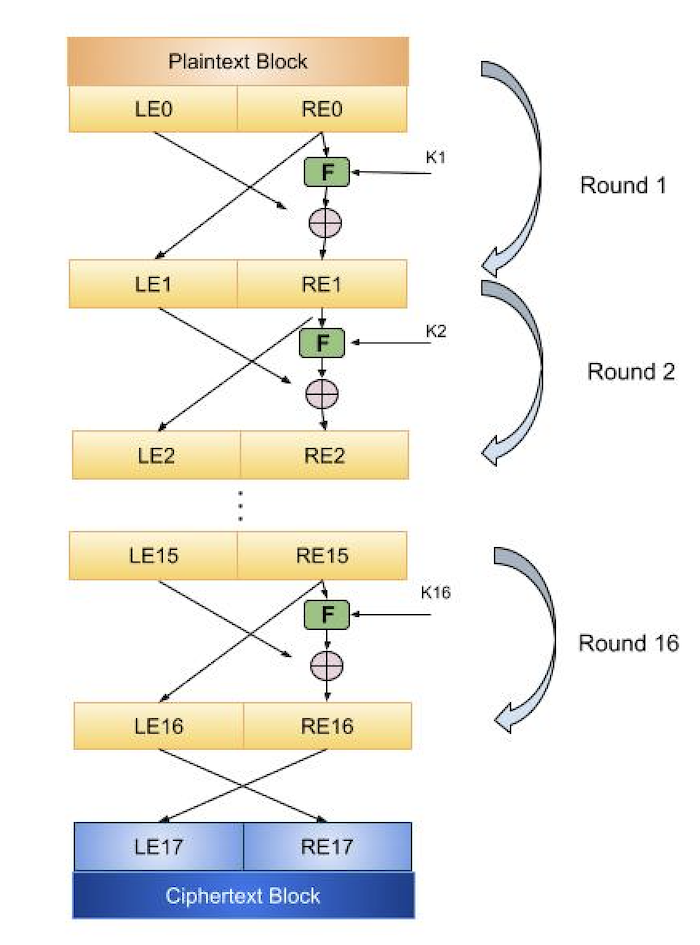
Feistel Block Cipher Encryption

  • 步骤 1 - 明文被分成固定大小的块，在此初始阶段一次只处理一个块。加密技术的两个输入是明文块和密钥 K。

  • 步骤 2 - 将明文块分成两部分。明文块将有两个不同的表示：LE0 代表块的左半部分，RE0 代表右半部分。为了创建密文块，明文块的两部分 (LE0 和 RE0) 将经历多轮明文处理。

对于每一轮，加密函数都应用于密钥 Ki 以及明文块的右半部分 REi。接下来，左半部分 LEj 与函数结果进行异或运算。在密码学中，逻辑运算符 XOR 用于比较两个输入位并生成一个输出位。对于下一轮，XOR 函数的输出成为新的右半部分 RE i+1。对于下一轮，左半部分 LEi+1 取代之前的右半部分 REi。

相同的函数（通过将轮函数应用于明文块的右半部分来实现替换函数）将在每一轮执行。块的左半部分用于对函数的输出进行异或运算。之后，使用置换函数交换这两半部分。给出下一轮的置换结果。实际上，Feistel 密码模型类似于前面讨论的 Shannon 结构，因为它交替使用替换和置换过程。

Feistel 密码的设计特征

使用分组密码时，会考虑以下 Feistel 密码设计特征：

  • 块大小 - 较大的块大小被认为可以使分组密码更安全。较大的块大小，但会减慢加密和解密过程的执行速度。分组密码通常包含 64 位块，而较新的版本，例如 AES（高级加密标准），则具有 128 位块。

  • 简单的分析 - 通过使分组密码易于分析，可以发现和修复密码分析漏洞，从而导致强算法的开发。

  • 密钥大小 - 与块大小类似，较高的密钥大小被认为更安全，但它们还会导致加密和解密过程花费时间才能完成。现代密码中，之前的 64 位密钥已被 128 位密钥取代。

  • 轮数 - 轮数也会影响分组密码的安全性。更多轮数可以提高安全性，但也会使加密更难以破解。因此，轮数取决于公司想要的数据保护类型。

  • 轮函数 - 复杂的轮函数会提高分组密码的安全性。

  • 子密钥生成函数 - 对于经验丰富的密码分析人员来说，具有更复杂的子密钥生成函数的密码更难以解密。

  • 快速的软件加密和解密 - 使用可以提高分组密码执行速度的软件是有利的。

解密

Feistel 密码模型对加密和解密使用相同的算法这一事实可能会让您感到惊讶。解密时需要注意以下一些重要准则：

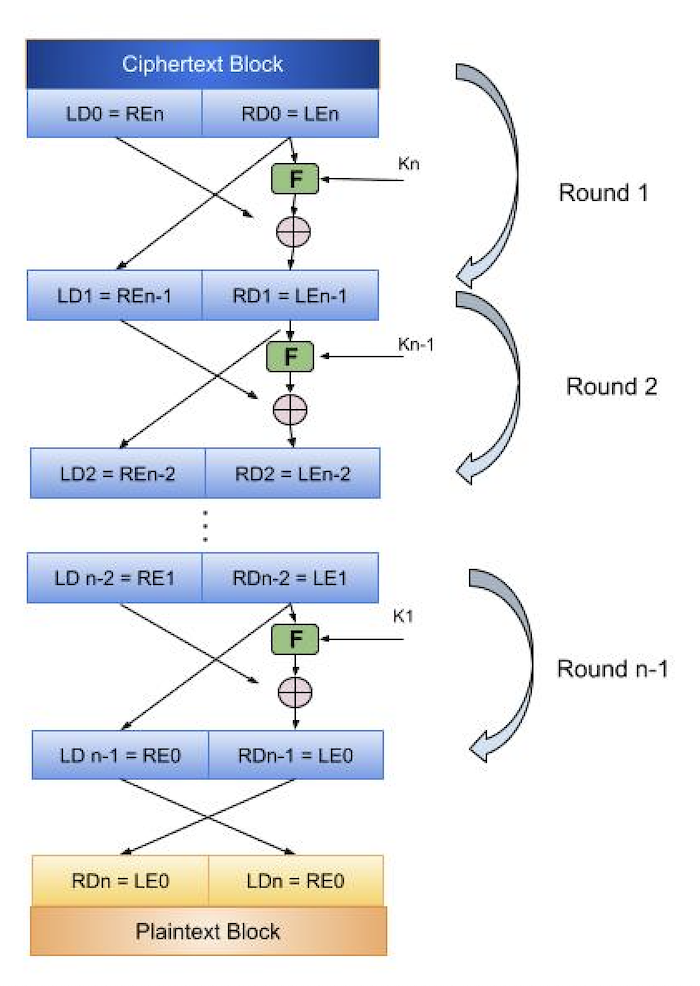
Feistel Block Cipher Decryption

如上图所示，加密文本块分为两部分，左部分 (LD0) 和右部分 (RD0)。

轮函数使用密钥Kn-1对密码块的右半部分进行运算，就像加密算法一样。密文块的左半部分与函数的结果进行异或运算。异或运算的结果成为新的右半部分（RD1），RD0与LD0交换位置，用于后续循环。事实上，每一轮都使用相同的函数，并在完成一定数量的轮次后得到明文块。

Python实现

让我们借助Python的binascii和random模块来实现Feistel分组密码：

此Python程序展示了Feistel密码算法的加密和解密过程。为了恢复原始明文，它首先加密输入，然后对其进行解密。

示例

import binascii
import random

def random_key(p):
   key = ""
   p = int(p)
   for _ in range(p):
      temp = random.randint(0, 1)
      temp = str(temp)
      key = key + temp
   return key

def exor_func(a, b):
   temp = ""
   for i in range(len(a)):
      if a[i] == b[i]:
         temp += "0"
      else:
         temp += "1"
   return temp

def convert_bin_to_dec(binary):
   string = int(binary, 2)
   return string

plaintext = "Hello Everyone"
print("Plain Text is:", plaintext)

plaintext_Ascii = [ord(x) for x in plaintext]
plaintext_Bin = [format(y, '08b') for y in plaintext_Ascii]
plaintext_Bin = "".join(plaintext_Bin)

n = len(plaintext_Bin) // 2
L1 = plaintext_Bin[0:n]
R1 = plaintext_Bin[n::]
m = len(R1)

K1 = random_key(m)
K2 = random_key(m)

f1 = exor_func(R1, K1)
R2 = exor_func(f1, L1)
L2 = R1

f2 = exor_func(R2, K2)
R3 = exor_func(f2, L2)
L3 = R2

bin_data = L3 + R3
str_data = ''

for i in range(0, len(bin_data), 7):
   temp_data = bin_data[i:i + 7]
   decimal_data = convert_bin_to_dec(temp_data)
   str_data = str_data + chr(decimal_data)

print("Cipher Text:", str_data)

L4 = L3
R4 = R3

f3 = exor_func(L4, K2)
L5 = exor_func(R4, f3)
R5 = L4

f4 = exor_func(L5, K1)
L6 = exor_func(R5, f4)
R6 = L5
plaintext1 = L6 + R6

plaintext1 = int(plaintext1, 2)
Rplaintext = binascii.unhexlify('%x' % plaintext1)
print("Decrypted Plain Text is: ", Rplaintext)

输出

Plain Text is: Hello Everyone
Cipher Text: '$Mau*ALLd;7B
Decrypted Plain Text is:  b'Hello Everyone'

总结

组织机构可以使用称为Feistel密码的流行加密设计理念来帮助保护其敏感数据。即使攻击者知道密码算法，强大的加密密码也应该阻止攻击者在没有密钥或密钥集的情况下破译密码明文。除了这种密码模型外，企业还应实施分层的网络安全方法，以帮助阻止攻击者窃取或泄露其机密数据。

打印页面
上一页
下一页
广告