密码学 - 希尔密码

在经典密码学的语境下，希尔密码使用多字母替换密码，这意味着在多个块级别上进行同质替换。这种多字母替换密码允许希尔密码轻松地使用二字母组（两字母块）、三字母组（三字母块）或任何其他多尺寸块来创建统一的密码。

希尔密码基于线性代数、高级矩阵（矩阵乘法和矩阵逆）和模算术原理。显然，它比其他密码更具有数学性。

希尔密码也是一种分组密码。分组密码使用确定性算法和对称密钥来加密一段文本。与流密码不同，它不需要一次加密一位。希尔密码是一种分组密码，这意味着它可以处理任何大小的块。

虽然希尔密码本质上是二字母组的，但它可以扩展到任何字母大小的乘法，增加了复杂性和可靠性，从而提高了使用效率。因为希尔密码的大部分问题和解决方案本质上都是数学性的，所以很容易精确地隐藏字母。

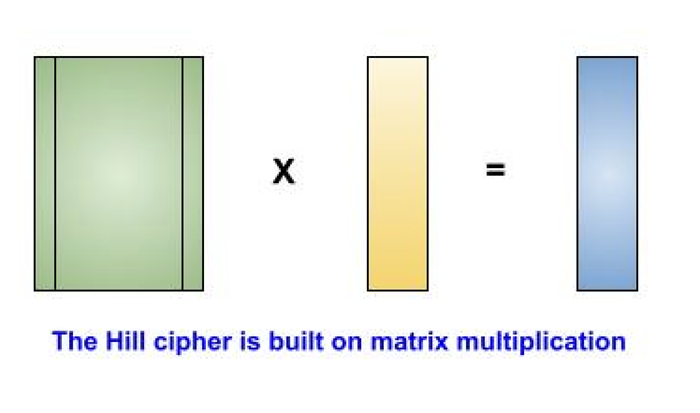
由于希尔密码相当复杂，让我们加密文本“CODE”，然后解密生成的密文来学习它的工作原理。为了使示例保持简单，我们将使用一种简单的替换方法，其中字母 A 映射到 0，B 映射到 1，依此类推，以符合 2x2 密钥矩阵。随着密钥矩阵大小的增加，希尔密码变得更加复杂。

历史

通过使用独特的方法和技术，密码学——安全通信的研究和实践——防止未经授权的人员或团队获取机密数据。保密性、数据完整性、身份验证等概念在现代密码学中非常重要。

著名的美国数学家莱斯特·S·希尔于 1929 年开发和改进了希尔密码技术。希尔密码使用多种数学技术，这些技术与传统密码学中的许多关键技术相关。

加密

使用希尔密码加密取决于以下操作：

E(K, P) = (K*P) mod 26

这里 K 是我们的密钥矩阵，P 是矢量化的明文。将这两个项进行矩阵乘法得到加密的密文。让我们一步一步地开始吧：

选择一个关键字来加密您的明文消息。让我们使用随机关键字“DCDF”。使用替换技术，将此项更改为数值 2x2 密钥矩阵。

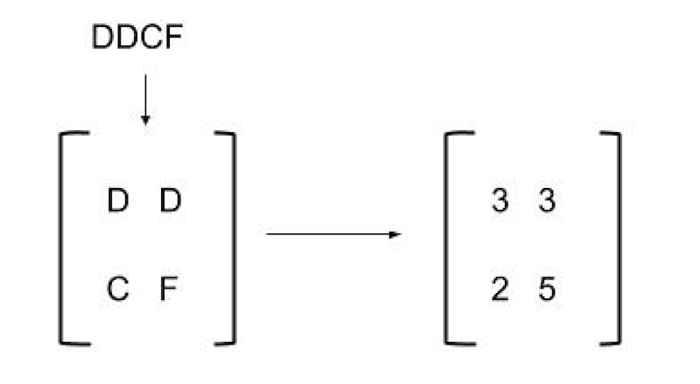
然后我们将明文消息转换为向量格式。因为我们的密钥矩阵是 2x2，矩阵乘法需要一个大小为 2x1 的向量。在我们的示例中，我们的消息有四个字母长，所以我们可以将其分成两个字母的块，然后进行替换以获得我们的明文向量。

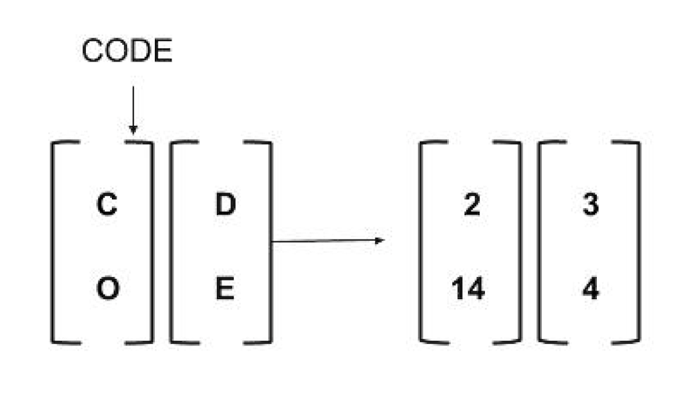
最终的密文“WWVA”可以通过将密钥矩阵与每个 2x1 明文向量进行矩阵相乘，取结果 2x1 向量的模 26，并将结果连接起来生成。所以对于 22 22 21 0 将是 WWVA。

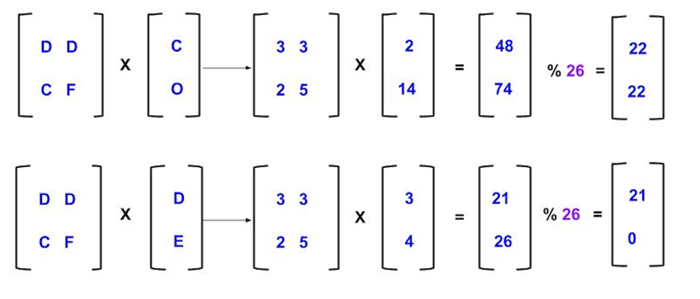
解密

希尔密码解密过程基于以下操作：

D(K, C) = (K^-1 *C) mod 26

这里 C 是矢量化的密文，K 是我们的密钥矩阵。通过将密钥矩阵的逆与密文进行矩阵相乘可以得到解密的明文。让我们使用“WWVA”作为我们的密文一步一步地进行：

我们首先计算密钥矩阵的逆。为此，我们必须使用模 26 来保持结果在 0 和 25 之间。因此，使用扩展欧几里得方法找到密钥矩阵行列式的模乘法逆。
之后，我们将密文的 2x1 块乘以密钥矩阵的逆，以恢复我们原始的明文消息“CODE”。

使用 Python 实现

这段 Python 代码借助 NumPy 进行矩阵运算，构建了希尔密码加密算法。它创建函数来根据给定的密钥定义密钥矩阵，使用生成的密钥矩阵加密消息，并进行希尔密码加密。hill_cipher 函数接受消息和密钥作为输入，创建密钥矩阵，也使用密钥矩阵加密消息，并将输出打印为密文。

示例

以下是使用 Python 的 numpy 库实现的希尔密码的 Python 实现：

import numpy as np

key_matrix = np.zeros((3, 3), dtype=int)
message_vector = np.zeros((3, 1), dtype=int)
cipher_matrix = np.zeros((3, 1), dtype=int)

def get_key_matrix(key):
   k = 0
   for i in range(3):
      for j in range(3):
         key_matrix[i][j] = ord(key[k]) % 65
         k += 1

def encrypt(message_vector):
   for i in range(3):
      cipher_matrix[i][0] = 0
      for x in range(3):
         cipher_matrix[i][0] += (key_matrix[i][x] * message_vector[x][0])
      cipher_matrix[i][0] = cipher_matrix[i][0] % 26

def hill_cipher(message, key):
   get_key_matrix(key)
   for i in range(3):
      message_vector[i][0] = ord(message[i]) % 65
   encrypt(message_vector)
   ciphertext = [chr(cipher_matrix[i][0] + 65) for i in range(3)]
   print("The Ciphertext:", "".join(ciphertext))

message = "DOG"
key = "YHGINUKER"
hill_cipher(message, key)

以下是上述示例的输出：

输入/输出

The Ciphertext: YOG

使用 Java 实现

这段 Java 代码使用希尔密码算法执行加密和解密。加密函数采用明文和密钥矩阵。返回加密的密文。解密函数采用密文和密钥矩阵。返回原始明文。行列式计算矩阵的行列式。并计算矩阵的伴随矩阵（余因子矩阵）。沿对角线转换矩阵以转置矩阵。

示例

请参见以下希尔密码的 Java 实现代码：

import java.util.Arrays;

public class HillCipher {
   private static final int MOD = 26;

   public static String encryptText(String plaintext, int[][] key) {
      plaintext = plaintext.toUpperCase().replaceAll(" ", "");
      int n = key.length;
      int padding = n - plaintext.length() % n;
      if (padding != n) {
         plaintext += "X".repeat(padding);
      }

      StringBuilder ciphertext = new StringBuilder();
      for (int i = 0; i < plaintext.length(); i += n) {
         int[] block = new int[n];
         for (int j = 0; j < n; j++) {
            block[j] = plaintext.charAt(i + j) - 'A';
         }
         int[] encryptedBlock = multiplyMatrix(key, block);
         for (int value : encryptedBlock) {
            ciphertext.append((char) (value + 'A'));
         }
      }
      return ciphertext.toString();
   }

   public static String decryptText(String ciphertext, int[][] key) {
      int determinant = determinant(key);
      int adjoint[][] = adjoint(key);
      int n = key.length;
      int[][] inverseKey = new int[n][n];

      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            inverseKey[i][j] = (adjoint[i][j] * determinant) % MOD;
            if (inverseKey[i][j] < 0) {
               inverseKey[i][j] += MOD;
            }
         }
      }
      return encryptText(ciphertext, inverseKey);
   }

   private static int[] multiplyMatrix(int[][] key, int[] block) {
      int n = key.length;
      int[] result = new int[n];
      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            result[i] += key[i][j] * block[j];
         }
         result[i] %= MOD;
      }
      return result;
   }

   private static int determinant(int[][] matrix) {
      if (matrix.length == 1) {
         return matrix[0][0];
      }
      int det = 0;
      for (int i = 0; i < matrix.length; i++) {
         int[][] minor = new int[matrix.length - 1][matrix.length - 1];
         for (int j = 1; j < matrix.length; j++) {
            for (int k = 0, col = 0; k < matrix.length; k++) {
               if (k == i) continue;
               minor[j - 1][col++] = matrix[j][k];
            }
         }
         det += Math.pow(-1, i) * matrix[0][i] * determinant(minor);
      }
      return det;
   }

   private static int[][] adjoint(int[][] matrix) {
      int n = matrix.length;
      int[][] adjoint = new int[n][n];
      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            int[][] minor = new int[n - 1][n - 1];
            for (int k = 0, row = 0; k < n; k++) {
               if (k == i) continue;
               for (int l = 0, col = 0; l < n; l++) {
                  if (l == j) continue;
                  minor[row][col++] = matrix[k][l];
               }
               row++;
            }
            adjoint[i][j] = (int) Math.pow(-1, i + j) * determinant(minor);
         }
      }
      return transpose(adjoint);
   }

   private static int[][] transpose(int[][] matrix) {
      int[][] result = new int[matrix.length][matrix.length];
      for (int i = 0; i < matrix.length; i++) {
         for (int j = 0; j < matrix.length; j++) {
            result[i][j] = matrix[j][i];
         }
      }
      return result;
   }

   public static void main(String[] args) {
      int[][] key = {{6, 24, 1}, {13, 16, 10}, {20, 17, 15}};
      String plaintext = "POINT";
      String ciphertext = encryptText(plaintext, key);
      System.out.println("The Encrypted Text: " + ciphertext);
      String decrypted = decryptText(ciphertext, key);
      System.out.println("The Decrypted Text: " + decrypted);
   }
}

以下是上述示例的输出：

输入/输出

The Encrypted Text: SFILBS
The Decrypted Text: POINTX

使用 C++ 实现

这段 C++ 代码实现了希尔密码的加密和解密算法。multiplyMatrix 函数将执行矩阵乘法。之后，determinant 函数将计算矩阵的行列式。然后，adjoint 函数计算矩阵的伴随矩阵。encrypt 函数使用密钥矩阵加密明文。decrypt 函数使用密钥矩阵解密密文。

示例

请参见下面的 Hill 密码 C++ 实现代码：

#include <iostream>
#include <vector>

using namespace std;

const int MOD = 26;

vector<vector<int>> multiplyMatrix(const vector<vector<int>>& key, const vector<int>& block) {
   int n = key.size();
   vector<vector<int>> result(n, vector<int>(1, 0));
   for (int i = 0; i < n; i++) {
      for (int j = 0; j < 1; j++) {
         for (int k = 0; k < n; k++) {
            result[i][j] += key[i][k] * block[k];
         }
         result[i][j] %= MOD;
      }
   }
   return result;
}

   int determinant(const vector<vector<int>>& matrix) {
      if (matrix.size() == 1) {
         return matrix[0][0];
      }
      int det = 0;
      int sign = 1;
      for (int i = 0; i < matrix.size(); i++) {
         vector<vector<int>> minor(matrix.size() - 1, vector<int>(matrix.size() - 1, 0));
         for (int j = 1; j < matrix.size(); j++) {
            for (int k = 0, col = 0; k < matrix.size(); k++) {
               if (k == i) continue;
               minor[j - 1][col++] = matrix[j][k];
            }
         }
         det += sign * matrix[0][i] * determinant(minor);
         sign *= -1;
      }
      return det;
   }

vector<vector<int>> adjoint(const vector<vector<int>>& matrix) {
      int n = matrix.size();
      vector<vector<int>> adjoint(n, vector<int>(n, 0));
      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            vector<vector<int>> minor(n - 1, vector<int>(n - 1, 0));
            for (int k = 0, row = 0; k < n; k++) {
               if (k == i) continue;
               for (int l = 0, col = 0; l < n; l++) {
                  if (l == j) continue;
                  minor[row][col++] = matrix[k][l];
               }
               row++;
            }
            adjoint[i][j] = determinant(minor) * ((i + j) % 2 == 0 ? 1 : -1);
         }
      }
      vector<vector<int>> result = adjoint;
      for (int i = 0; i < n; i++) {
         for (int j = i + 1; j < n; j++) {
            swap(result[i][j], result[j][i]);
         }
      }
      return result;
   }

   string encrypt(const string& plaintext, const vector<vector<int>>& key) {
      string modifiedPlaintext = plaintext;
      int n = key.size();
      int padding = n - modifiedPlaintext.size() % n;
      if (padding != n) {
         modifiedPlaintext += string(padding, 'X');
      }

      string ciphertext = "";
      for (int i = 0; i < modifiedPlaintext.size(); i += n) {
         vector<int> block(n, 0);
         for (int j = 0; j < n; j++) {
            block[j] = modifiedPlaintext[i + j] - 'A';
         }
         vector<vector<int>> encryptedBlock = multiplyMatrix(key, block);
         for (const auto& row : encryptedBlock) {
            for (int value : row) {
               ciphertext += (char) (value + 'A');
            }
         }
      }
      return ciphertext;
   }

   string decrypt(const string& ciphertext, const vector<vector<int>>& key) {
      int det = determinant(key);
      vector<vector<int>> adj = adjoint(key);
      vector<vector<int>> inverseKey = key;

      int n = key.size();
      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            inverseKey[i][j] = (adj[i][j] * det) % MOD;
            if (inverseKey[i][j] < 0) {
               inverseKey[i][j] += MOD;
            }
         }
      }
      return encrypt(ciphertext, inverseKey);
   }

int main() {
   vector<vector<int>> key = {{6, 24, 1}, {13, 16, 10}, {20, 17, 15}};
   string plaintext = "HELLO";
   string ciphertext = encrypt(plaintext, key);
   cout << "The Encrypted Text: " << ciphertext << endl;
   string decrypted = decrypt(ciphertext, key);
   cout << "The Decrypted Text: " << decrypted << endl;
   return 0;
}

以下是上述示例的输出：

输入/输出

The Encrypted Text: TFJJZX
The Decrypted Text: HELLOX

优势

Hill 密码加密算法具有以下优势：

安全性 − Hill 密码使用字母块而不是单个字母进行运算，因此比其他传统的替换密码更安全。它不易受到使用频率分析的攻击。
灵活性 − Hill 密码可以加密和解密包含大写字母、小写字母、标点符号和空格的消息。由于其适应性强，它可以用于加密各种文本文件。
数学背景 − Hill 密码基于线性代数的思想，为理解和创建高级加密方法提供了框架。它提供了一个研究加密技术和矩阵之间关系的机会。
密钥强度 − 加密密钥矩阵的大小和不可预测性直接影响 Hill 密码的安全性。通过使用更大的密钥矩阵可以提高加密强度，这将使未经授权的方更难以解密消息。
复杂性 − Hill 密码在没有加密密钥的情况下更难理解，因为它在加密过程中使用了矩阵运算。这进一步提高了算法的安全性。

Hill 密码的安全性

当使用 2x2 矩阵时，Hill 密码很容易破解。然而，对于提供 256 种可能数字的现代加密系统而言，Hill 密码效率非常低。

先前已经证明，Hill 密码的线性相关性在防御已知明文攻击方面存在已知的漏洞。由于 Hill 密码仅使用常规的代数方法求解，因此任何具有线性密文对的系统都可以轻松破解 Hill 密码矩阵。

然而，增加矩阵乘法的次数并不能显著增强系统安全性。另一方面，它可以与非线性过程结合使用以支持扩散。像 AES 这样的现代高级加密技术使用不同的扩散来更好地增强系统安全性。

Lester S. Hill 开发了一种用于 6x6 矩阵密码的专用机器，该机器被证明安全性有所提高。但由于其主要设置不可调整，其实际应用受到限制。

打印页面