密码学 - RC4 算法

上一页
下一页

Rivest 密码 4 被称为 RC4。这种名为 RC4 的流密码是由 Ron Rivest 于 1987 年创建的。RC4 是一种流密码，它逐位加密数据。在所有流密码中，RC4 因其简单性和速度而成为使用最广泛的一种。

尽管 RC4 以其速度和易于在软件中使用而闻名，但已发现它存在许多漏洞，使其不安全。如果未删除输出密钥流的开头，或者使用链接或非随机密钥，则它极易受到攻击。特别是，RC4 的使用导致了 WEP 等相对不安全的协议的产生。

2015 年，有传言称某些国家密码学组织可能会破解 RC4，如果它用于 TLS 协议的话。互联网工程任务组的 RFC 7465 禁止在 TLS 中使用 RC4，Mozilla 和 Microsoft 也提出了类似的建议。

RC4 如何工作？

RC4 生成密钥流或伪随机比特流。这可以用于加密，方法是使用按位异或与明文组合，就像任何其他流密码一样。由于异或是一种对称运算，因此解密也遵循相同的过程。

该密码使用隐藏的内部状态生成密钥流，该状态分为两部分：

  • 所有 256 个可用字节都被置换。
  • 每个索引指针有八位。

已知密钥调度方法使用可变长度密钥（通常在 40 到 256 位之间）来初始化置换。然后使用伪随机生成方法生成比特流。

以下是使用 XOR 加密的图像。

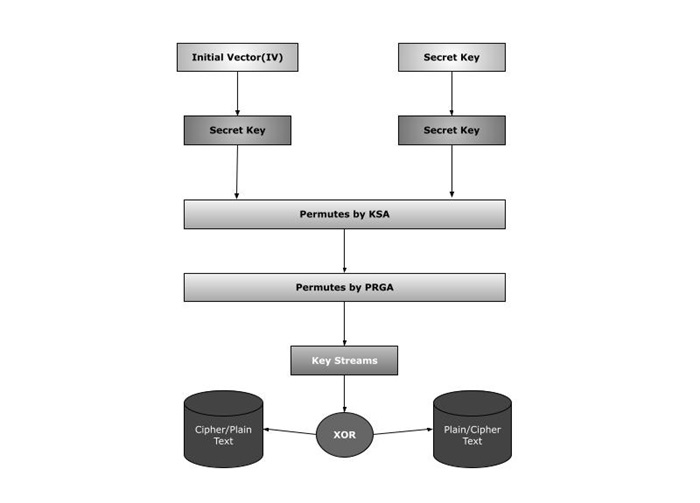
RC4 Algorithm

加密

  • 用户输入明文和密钥。
  • 加密算法使用 KSA 和 PRGA 算法为输入的密钥生成密钥流。
  • 生成的密钥流与明文进行异或运算。由于 RC4 是流密码，因此使用逐字节异或来创建密文。
  • 现在，目标接收者以加密形式接收此密文。

解密

  • 密文使用相同的逐字节异或方法解密。

密钥生成

使用长度从 1 到 256 字节不等的可变长度密钥初始化包含元素 S[0] 到 S[255] 的 256 字节状态向量 S。通过仔细选择 255 个条目中的一个来创建用于加密和解密的字节 k，之后 S 中的条目执行另一次置换。

密钥调度

通过将 S 条目的值设置为从 0 到 255 的升序来生成临时向量 T。如果其长度为 256 字节，则将密钥 k 分配给 T。否则，对于长度为 (k-len) 字节的密钥，T 的前 k-len 个元素从 K 复制，然后根据需要重复 K 以填充 T。以下是该概念的表示：

首先初始化数组 S 和 T。接下来，我们使用数组 K 来计算数组 T。最后，我们将数组 T 给出的方法应用于数组 S 的第一次置换。

示例

// Initialize array S
int[] S = new int[256];
for (int i = 0; i < 256; i++) {
   S[i] = i;
}

// Calculate array T using array K
int[] T = new int[256];
for (int i = 0; i < 256; i++) {
   T[i] = K[i % K.length - len];
}

这段 Java 代码使用 0 到 255 的值初始化数组 S，然后使用对数组 K 的模运算来计算数组 T。

# Initializing arrays S and T
S = list(range(256))
T = [0] * 256

# Calculating array T using array K
for i in range(256):
   T[i] = K[i % len(K) - len]

# Performing initial permutation of array S using array T
j = 0
for i in range(256):
   j = (j + S[i] + T[i]) % 256
   # Swap S[i] and S[j]
   S[i], S[j] = S[j], S[i]

设置向量 S 后，将不再使用输入密钥。在此步骤中，使用由 S 的当前配置确定的方案将每个 S[i] 算法字节与 S 中的不同字节交换。到达 S[255] 后，该方法继续，再次从 S[0] 开始。

# Initialize array S with values from 0 to 255
S = list(range(256))

# Start swapping process
i = 0
j = 0
for _ in range(256):
   i = (i + 1) % 256
   j = (j + S[i]) % 256
   # Swap S[i] and S[j]
   S[i], S[j] = S[j], S[i]

RC4 的特点

  • RC4 使用对称密钥，这意味着相同的密钥用于加密和解密。
  • RC4 是流密码算法的一个示例，这意味着数据一次一个字节地进行加密和解密。密文是通过将它生成的伪随机位密钥流与明文进行异或运算创建的。
  • RC4 允许 40 位到 2048 位的不同密钥大小，因此它可以灵活适应各种安全需求。
  • RC4 加密技术快速有效，非常适合低功耗设备和需要高速发送数据的应用程序。
  • RC4 广泛用于许多不同的应用程序，例如文件加密、虚拟专用网络 (VPN)、安全套接字层 (SSL) 和无线网络。
  • RC4 容易受到多种攻击，其中一种攻击是密钥流的初始几个字节中的偏差，可用于检索密钥。因此，不再建议在新应用程序中使用 RC4。

使用 Python 实现

现在我们将借助Python实现RC4。

示例

# Function for encryption
def encrypt_rc4():

   global secret_message, secret_key, n

   # Given text and key
   secret_message = "101101100110"
   secret_key = "001010010010"

   # n is the number of bits 
   n = 3

   print("Secret message : ", secret_message)
   print("Secret key : ", secret_key)
   print("n : ", n)

   print(" ")

   # The initial state vector array
   S = [i for i in range(0, 2**n)]
   print("S : ", S)

   key_list = [secret_key[i:i + n] for i in range(0, len(secret_key), n)]

   # Convert key stream to decimal
   for i in range(len(key_list)):
      key_list[i] = int(key_list[i], 2)

   # Convert secret message to decimal
   global pt

   pt = [secret_message[i:i + n] for i in range(0, len(secret_message), n)]

   for i in range(len(pt)):
      pt[i] = int(pt[i], 2)

   print("Secret message (in array form): ", pt)

   # Making key stream equal to the length of state vector
   diff = int(len(S)-len(key_list))

   if diff != 0:
      for i in range(0, diff):
         key_list.append(key_list[i])

   print("Key list : ", key_list)
   print(" ")

   # Perform the KSA algorithm
   def key_scheduling_algorithm():
      j = 0
      N = len(S)
		
      # Iterate over the range [0, N]
      for i in range(0, N):
		
         # Find the key
         j = (j + S[i]+key_list[i]) % N
			
         # Update S[i] and S[j]
         S[i], S[j] = S[j], S[i]
         print(i, " ", end ="")
			
         # Print S
         print(S)

      initial_permutation_array = S
		
      print(" ")
      print("Initial permutation array : ",
         initial_permutation_array)

   print("KSA process : ")
   print(" ")
   key_scheduling_algorithm()
   print(" ")

   # Perform PGRA algorithm
   def pseudo_random_generation_algorithm():

      N = len(S)
      i = j = 0
      global key_stream
      key_stream = []

      # Iterate over [0, length of pt]
      for k in range(0, len(pt)):
         i = (i + 1) % N
         j = (j + S[i]) % N
			
         # Update S[i] and S[j]
         S[i], S[j] = S[j], S[i]
         print(k, " ", end ="")
         print(S)
         t = (S[i]+S[j]) % N
         key_stream.append(S[t])

      # Print the key stream
      print("Generated key stream : ", key_stream)
      print(" ")

   print("Key stream generation : ")
   print(" ")
   pseudo_random_generation_algorithm()

   # Performing XOR between generated key stream and secret message
   def perform_xor():
      global cipher_text
      cipher_text = []
      for i in range(len(pt)):
         c = key_stream[i] ^ pt[i]
         cipher_text.append(c)

   perform_xor()

   # Convert the encrypted text to bits form
   encrypted_to_bits = ""
   for i in cipher_text:
      encrypted_to_bits += '0'*(n-len(bin(i)[2:]))+bin(i)[2:]

   print(" ")
   print("Cipher text : ", encrypted_to_bits)

# Execute function
encrypt_rc4()

print("*********************************************************")

# Function for decryption of data
def decrypt_rc4():

   # The initial state vector array
   S = [i for i in range(0, 2**n)]

   key_list = [secret_key[i:i + n] for i in range(0, len(secret_key), n)]

   # Convert key stream to decimal
   for i in range(len(key_list)):
      key_list[i] = int(key_list[i], 2)

   # Convert secret message to decimal
   global pt

   pt = [secret_message[i:i + n] for i in range(0, len(secret_message), n)]

   for i in range(len(pt)):
      pt[i] = int(pt[i], 2)

   # Making key stream equal to the length of state vector
   diff = int(len(S)-len(key_list))

   if diff != 0:
      for i in range(0, diff):
         key_list.append(key_list[i])

   print(" ")

   # KSA algorithm
   def key_scheduling_algorithm():
      j = 0
      N = len(S)
		
      # Iterate over the range [0, N]
      for i in range(0, N):
         j = (j + S[i]+key_list[i]) % N
			
         # Update S[i] and S[j]
         S[i], S[j] = S[j], S[i]
         print(i, " ", end ="")
         print(S)

      initial_permutation_array = S
      print(" ")
      print("Initial permutation array : ",
         initial_permutation_array)

   print("KSA process : ")
   print(" ")
   key_scheduling_algorithm()
   print(" ")

   # Perform PRGA algorithm
   def pseudo_random_generation_algorithm():

      N = len(S)
      i = j = 0
      global key_stream
      key_stream = []

      # Iterate over the range
      for k in range(0, len(pt)):
         i = (i + 1) % N
         j = (j + S[i]) % N
			
         # Update S[i] and S[j]
         S[i], S[j] = S[j], S[i]
         print(k, " ", end ="")
         print(S)
         t = (S[i]+S[j]) % N
         key_stream.append(S[t])

      print("Generated key stream : ", key_stream)
      print(" ")

   print("Key stream generation : ")
   print(" ")
   pseudo_random_generation_algorithm()

   # Perform XOR between generated key stream and cipher text
   def perform_xor():
      global original_text
      original_text = []
      for i in range(len(cipher_text)):
         p = key_stream[i] ^ cipher_text[i]
         original_text.append(p)

      perform_xor()

   # convert the decrypted text to the bits form
   decrypted_to_bits = ""
   for i in original_text:
      decrypted_to_bits += '0'*(n-len(bin(i)[2:]))+bin(i)[2:]

   print(" ")
   print("Decrypted text : ",
      decrypted_to_bits)

# execute function
decrypt_rc4()

以下是上述示例的输出：

输入/输出

Secret message :  101101100110
Secret key :  001010010010
n :  3
 
S :  [0, 1, 2, 3, 4, 5, 6, 7]
Secret message (in array form):  [5, 5, 4, 6]
Key list :  [1, 2, 2, 2, 1, 2, 2, 2]
 
KSA process : 
 
0  [1, 0, 2, 3, 4, 5, 6, 7]
1  [1, 3, 2, 0, 4, 5, 6, 7]
2  [1, 3, 7, 0, 4, 5, 6, 2]
3  [1, 0, 7, 3, 4, 5, 6, 2]
4  [1, 0, 7, 3, 6, 5, 4, 2]
5  [1, 0, 7, 3, 6, 5, 4, 2]
6  [1, 0, 7, 4, 6, 5, 3, 2]
7  [1, 0, 7, 4, 6, 5, 3, 2]
 
Initial permutation array :  [1, 0, 7, 4, 6, 5, 3, 2]
 
Key stream generation : 
 
0  [0, 1, 7, 4, 6, 5, 3, 2]
1  [0, 1, 2, 4, 6, 5, 3, 7]
2  [0, 1, 2, 4, 6, 5, 3, 7]
3  [0, 6, 2, 4, 1, 5, 3, 7]
Generated key stream :  [1, 1, 0, 7]
 
 
Cipher text :  100100100001
*********************************************************
KSA process : 
 
0  [1, 0, 2, 3, 4, 5, 6, 7]
1  [1, 3, 2, 0, 4, 5, 6, 7]
2  [1, 3, 7, 0, 4, 5, 6, 2]
3  [1, 0, 7, 3, 4, 5, 6, 2]
4  [1, 0, 7, 3, 6, 5, 4, 2]
5  [1, 0, 7, 3, 6, 5, 4, 2]
6  [1, 0, 7, 4, 6, 5, 3, 2]
7  [1, 0, 7, 4, 6, 5, 3, 2]
 
Initial permutation array :  [1, 0, 7, 4, 6, 5, 3, 2]
 
Generated key stream :  [1, 1, 0, 7]
 
Key stream generation : 
 
0  [0, 1, 7, 4, 6, 5, 3, 2]
1  [0, 1, 2, 4, 6, 5, 3, 7]
2  [0, 1, 2, 4, 6, 5, 3, 7]
3  [0, 6, 2, 4, 1, 5, 3, 7]
 
Decrypted text :  101101100110

RC4的用途

多年来，RC4越来越受欢迎，并成为商业应用中的标准。它以简单、快速和廉价的加密技术而闻名。

RC4的主要优点是易于实现和使用，以及其运行和部署速度快。它能够高效快速地处理大型数据流。在内存使用方面，RC4流密码也很高效。

然而，由于近年来发现了缺陷和网络攻击的证据，人们呼吁停止使用RC4加密算法。还发现了其他缺点，例如无法处理小型数据流以及在实施新系统之前需要进行额外调查。

互联网工程任务组 (IETF) 在 2015 年禁止在 TLS 协议中使用 RC4。由于威胁漏洞，微软和Mozilla也发布了限制使用RC4的建议。许多基于RC4的生态系统，例如WEP、WPA、BitTorrent协议加密、Microsoft点对点加密等。

RC4A是RC4功能更强大的变体。RC4A+是RC4的修改版本，具有更复杂的3阶段密钥调度，比基本RC4长1.7倍。

RC4的优点

以下是使用RC4时需要考虑的一些RC4优点：

  • RC4是一种非常快速且高效的加密方法，使其适用于需要这些特性的场景。
  • 由于RC4是一种相当基本的算法，因此可以在硬件或软件中轻松实现。
  • RC4是动态的，并且可以适应各种安全需求，因为它允许不同的密钥大小。
  • RC4 广泛用于许多不同的应用程序，例如文件加密、虚拟专用网络 (VPN)、安全套接字层 (SSL) 和无线网络。

RC4的缺点

使用RC4时，我们需要考虑一些严重的缺点：

  • 由于许多已追踪到的漏洞，RC4不适用于新的应用程序。例如，可以通过利用密钥流前几个字节中存在的偏差来恢复密钥。
  • 与AES或ChaCha20等其他加密算法相比，由于其架构中存在一些内置漏洞，RC4安全性较低。
  • RC4的2048位最大密钥长度对于某些需要更高级别加密的应用程序可能不够。
  • 由于其漏洞和缺陷，不再建议在新应用程序中使用RC4。取而代之的是，需要使用两种更安全的流密码算法：AES-CTR或ChaCha20。

RC4和WEP

WEP（有线等效隐私）是一种用于保护无线网络的安全机制。它具有与有线网络类似的隐私和安全功能。WEP在Wi-Fi的早期被广泛使用，但它存在一些已知的漏洞，使得它非常容易受到攻击。这些弱点包括弱密钥调度机制（基于RC4）、短初始化向量（IV）和缺乏密钥管理工具。

在WEP中，数据首先使用RC4技术加密，然后通过无线网络发送。由于WEP协议中的弱点，网络安全很容易受到各种攻击的影响，例如Fluhrer-Mantin-Shamir (FMS)攻击和KoreK攻击，这些攻击可以检索WEP密钥。

WEP是一种强大的流密码，但RC4的实现引入了问题。因此，更安全的加密协议，如WPA（Wi-Fi保护访问）和WPA2最终取代了WEP。

打印页面
上一页
下一页
广告