密码学 - Camellia 加密算法

Camellia 是一种对称密钥分组密码，使用 128 位的块大小和 128、192 和 256 位的密钥大小。三菱电机和日本的 NTT 合作开发了它。

该密码提供与高级加密标准相当的安全性和处理能力。

该密码旨在与软件和硬件一起使用，范围从低成本智能卡到高速网络系统。它是传输层安全 (TLS) 加密协议的一部分，用于保护通过计算机网络（如互联网）的通信。

Camellia 的设计

Camellia 是一种 Feistel 密码，具有 18 轮（128 位密钥）或 24 轮（192 位或 256 位密钥）。每六轮应用一个逻辑转换层，称为“FL 函数”或其逆。Camellia 使用四个 8x8 位 S 盒进行输入和输出仿射变换以及逻辑运算。

该密码还使用输入和输出密钥白化。扩散层应用基于分支数为 5 的矩阵的线性变换。

算法

• Camellia 是一种对称分组密码，密钥长度为 128、192 或 256 位。明文和密文块的长度始终为 128 位。
• 以下描述使用 Camellia 文档中变量和函数的原始名称来描述其算法。
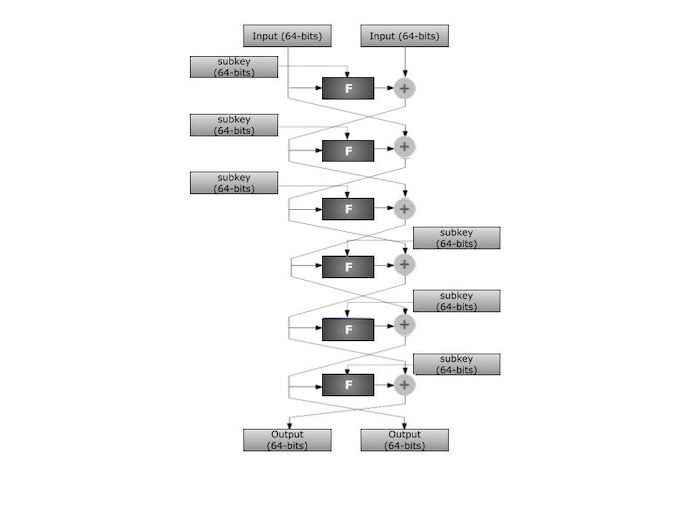
• 算法最重要的元素是 F 函数。它们用于密钥加密和解密，以及辅助变量的创建。F 函数接受 128 位输入，将其与子密钥 k_i 的位组合，并生成 128 个新位。F 函数中位的修改通常称为算法中的一轮。F 函数调用被分组到块中。每个块有六轮。
• 六轮块（对 F 函数的六次调用的块）由对 FL 函数和 FL^-1 函数的调用分隔。它们操作 64 位数据块，并使用子密钥 kl_i 将它们组合。
• 加密和解密算法都将重复上面概述的六轮块。重复次数由当前密钥的长度决定。
• 对于 128 位密钥，重复 6 轮块三次。对于 192 位或 256 位密钥，重复块四次。
• 此外，在加密和解密方法的开始和结束时，数据位将添加到子密钥 kw_i 的位。
• 子密钥用于加密或解密每个数据块，是在另一种方法中生成的。每个块的密钥生成数十个子密钥。它们在主算法的各个阶段使用。

密钥调度

Camellia 密码中使用的密钥可以是 128、192 或 256 位。加密数据块需要创建一些辅助变量，然后根据密钥位创建子密钥。每个子密钥长 64 位。

首先，计算两个 128 位变量（K_L 和 K_R）和四个 64 位变量（K_LL、K_LR、K_RL 和 K_RR）。以下等式描述了这些变量之间的关系 -

• K_LL 等于 K_L 的 64 个左位
• K_LR 等于 K_L 的 64 个右位
• K_RL 等于 K_R 的 64 个左位
• K_RR 等于 K_R 的 64 个右位

其余连接应使用密钥 K 的长度来识别。

• 对于 128 位密钥：K_L 等于 K 且 K_R 等于 0
• 对于 192 位密钥：K_L 等于 K 的 128 个左位，K_RL 等于 K 的 64 个右位，K_RR 等于 ~K_RL（位的否定）。
• 对于 256 位密钥：K_L 等于 K 的 128 个左位，K_R 等于 K 的 128 个右位

接下来，使用前面的辅助变量作为基础，可以计算两个新的变量：K_A 和 K_B。它们都长 128 位。当且仅当密钥为 192 位或 256 位时，K_B 不为零。在构建 K_A 和 K_B 时，应使用六个辅助常数值，称为 ∑_i。

最后，应该根据四个最近创建的 128 位长变量 K_L、K_R、K_A 和 K_B 计算所有 64 位密钥子密钥 k_i、kw_i 和 kl_i。Camellia 算法在加密和解密的每个阶段都使用子密钥。

Camellia 加密的安全性

山茶花加密算法被认为是一种先进且安全的密码算法。截至目前，人们认为使用蛮力攻击密钥来破解它非常困难，即使使用较小的密钥大小选项（128 位）也是如此。没有已知的成功攻击报告能够显著破解该密码算法。这款日本密码算法在处理能力和安全级别方面与 AES/Rijndael 密码算法相当。

山茶花是一种块密码，其特征在于多元多项式的最小系统 -

• 山茶花（和 AES）的 S 盒可以使用 80 项中的 23 个二次方程系统来定义。
• 基本密钥编排可以使用 768 个变量中的 1120 个方程来表示，其中包含 3328 个线性和二次项。
• 完整的块密码可以用 2816 个变量中的 5104 个方程来描述，其中包含 14592 个线性和二次项。
• 总共需要 3584 个变量中的 6224 个方程，其中包含 17920 个线性和二次项。
• 自由项的数量为 11696，这与 AES 几乎相同。

如果攻击可行，这些特性将使将来有可能使用代数攻击（如扩展稀疏线性化）来破解山茶花（和 AES）。

优势

以下是山茶花加密的优势 -

• 山茶花加密非常安全，并且能够抵御各种各样的密码攻击。它具有较大的密钥大小和复杂循环设计，这使得它能够高度抵御蛮力攻击。
• 山茶花具有适应性，可用于各种密码任务，例如数据加密、数字签名和密钥交换协议。其多功能性使其适合各种安全需求。
• 尽管山茶花拥有出色的安全特性，但它使用的计算资源相对较少。它可以在软件和硬件平台上高效实现，使其适合各种应用。
• 山茶花已由国际标准化组织（ISO）和互联网工程任务组（IETF）等国际组织标准化。
• 山茶花与现有的密码基础设施和协议兼容，可以轻松集成到现有系统中，无需进行重大更改。

劣势

以下是山茶花的一些劣势 -

• 山茶花可能不像其他对称密钥加密算法（如 AES）那样知名或广泛使用。这可能导致可用资源、库和支持比更成熟的算法少。
• 尽管山茶花是一种常见的加密技术，但在某些应用和行业中其使用可能受到限制。一些企业可能更倾向于使用 AES 等知名算法，因为熟悉性和信任度。
• 虽然山茶花旨在安全，但没有任何加密方法能够完全免受漏洞的影响。随着计算能力和密码攻击的改进，随着时间的推移可能会发现山茶花中的其他问题，这可能会危及其安全性。