密码学 - 仿射密码

上一页
下一页

现在我们将学习仿射密码及其加密和解密算法。仿射密码是单字母替换密码的一个例子。它是一种加密策略。它也像一个秘密代码，将敏感内容转换为编码形式。

在仿射密码中，消息中的每个字母都通过遵循一个简单的数学公式替换为另一个字母。在这个算法中，我们将字母在字母集中的位置乘以一个数字，然后再加上另一个数字。此过程更改消息，以便只有知道正确数字的人才能将其翻译回其原始形式。

由于加密策略基本上是数学的，因此它与我们已经看到的其他情况略有不同。整个过程依赖于模m运算，其中m是字符集的长度。我们通过对明文字符应用方程来转换明文。

仿射密码加密

加密过程的第一步是将明文字母集中的每个字母转换为其在 0 到 M-1 范围内的对应数字。完成此操作后，每个字母的加密过程由下式给出：

E(x) = (Ax + B) mod M

其中，

  • E 是加密消息。

  • x 是字母在字母集中的位置（例如，A=0，B=1，C=2，…，Z=25）

  • A 和 B 是密码的密钥。这表明我们在将明文字母的数值乘以 A 后，将 B 加到结果中。

  • M 表示模。

（也就是说，当我们将大数除以字母集的长度时，我们找到余数部分。这确保了我们的新字母仍然在字母表内）。

仿射密码解密

当我们必须使用仿射密码加密系统解密密文时，我们将不得不执行与加密相反的过程。第一步是将每个密文字母转换回其数值，就像我们在转换消息时所做的那样。

然后，要解密每个数字，我们使用以下公式：

D(x)= C(x − B) mod M

其中，

  • D 代表解密消息。

  • x 表示我们从密文字母获得的数字。

  • B 表示我们在加密时添加以移动字母的数字。

  • C 是一个特殊的数字，称为 A 的模乘法逆元。这是一个数字，当我们将其乘以 A 并不断减去字母表的长度时，我们将得到 1。

  • M 是模或字母的长度。

让我们看看下面的图片，以简单的方式理解加密和解密过程。

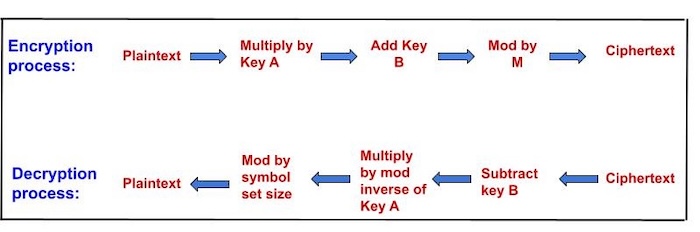
basic implementation of affine cipher

使用 Python 实现

现在，我们将使用不同的方法实现使用 Python 的仿射加密和解密程序：

  • 使用字典映射

  • 使用预定义密钥

因此，我们将在以下部分中看到所有上述方法及其在 Python 中的实现：

使用字典映射

在这个例子中，我们将使用字典映射来使用 Python 创建仿射密码算法。字典映射的过程需要在解密或加密的情况下将每个字母转换为其等效字母。

我们的加密和解密数学公式为仿射密码中的这种映射提供了起点。字母表的原始字母用作字典的键，而其加密或解密版本用作值。可以使用代码中此字典访问明文或密文中每个字母的加密或解密字母。

示例

以下是使用字典映射的仿射密码加密和解密算法的 Python 实现。请查看下面的代码：

# Encryption function
def affine_encrypt(text, a, b):
   encrypted_text = ""
   for char in text:
      if char.isalpha():
         if char.isupper():
            encrypted_text += chr(((a * (ord(char) - ord('A')) + b) % 26) + ord('A'))
         else:
            encrypted_text += chr(((a * (ord(char) - ord('a')) + b) % 26) + ord('a'))
      else:
         encrypted_text += char
   return encrypted_text

# Decryption function
def affine_decrypt(text, a, b):
   decrypted_text = ""
   m = 26
   a_inv = pow(a, -1, m)
   for char in text:
      if char.isalpha():
         if char.isupper():
            decrypted_text += chr(((a_inv * (ord(char) - ord('A') - b)) % 26) + ord('A'))
         else:
            decrypted_text += chr(((a_inv * (ord(char) - ord('a') - b)) % 26) + ord('a'))
      else:
         decrypted_text += char
   return decrypted_text

# plain text message and keys
plain_text = "Nice to meet you!"
a = 5
b = 8

encrypted_text = affine_encrypt(plain_text, a, b)
print("Our Encrypted text:", encrypted_text)

decrypted_text = affine_decrypt(encrypted_text, a, b)
print("Our Decrypted text:", decrypted_text)

以下是上述示例的输出：

输入/输出
Our Encrypted text: Vwsc za qccz yae!
Our Decrypted text: Nice to meet you!

使用预定义密钥

此代码执行仿射密码过程以编码和解码内容。它在 KEY 变量中使用预定义密钥进行加密和解密。此变量是一个包含三个值的元组：（7, 3, 55）。这些值显示仿射密码的加密和解密密钥。我们还将有另一个变量称为 DIE，它表示字符集大小 (128)。

示例

以下是使用预定义密钥的仿射密码加密和解密算法的 Python 实现。查看下面的代码：

# Affine cipher Class
class affine_cipher(object):
   DIE = 128
   KEY = (7, 3, 55)

   def __init__(self):
     pass

   def encryptChar(self, char):
      K1, K2, kI = self.KEY
      return chr((K1 * ord(char) + K2) % self.DIE)

   def encrypt(self, string):
      return "".join(map(self.encryptChar, string))

   def decryptChar(self, char):
      K1, K2, KI = self.KEY
      return chr((KI * (ord(char) - K2)) % self.DIE)

   def decrypt(self, string):
      return "".join(map(self.decryptChar, string))

affine = affine_cipher()
print("Our Encrypted Text: ", affine.encrypt('Affine Cipher'))
print("Our Decrypted Text: ", affine.decrypt('JMMbFcXb[F!'))

以下是上述示例的输出：

输入/输出
Our Encrypted Text:  JMMbFcXb[F!
Our Decrypted Text:  Affine Cipher

使用 Java 实现

本实现将使用Java编程语言来使用仿射密码加密和解密消息。因此，我们将在这里使用两个密钥，第一个是乘法密钥 (A)，第二个是加法密钥 (B)。这些密钥将用于混合给定消息中的字母，使其保密。对于解密消息，将使用一种称为模乘法逆的特殊数学公式来撤消加密。

示例

因此，下面给出了使用Java实现仿射密码的方法：

public class AffineCipher {
    
   static final int A = 17; // Multiplicative Key
   static final int B = 20; // Additive Key

   // Function to find modular multiplicative inverse
   static int modInverse(int a, int m) {
      for (int x = 1; x < m; x++) {
         if (((a % m) * (x % m)) % m == 1) {
            return x;
         }
      }
      return -1; // If inverse is not there
   }
    
   // Function to encrypt plaintext
   static String encryptMessage(String pt) {
      StringBuilder ciphertext = new StringBuilder();
      for (int i = 0; i < pt.length(); i++) {
         char ch = pt.charAt(i);
         if (Character.isLetter(ch)) {
            if (Character.isUpperCase(ch)) {
               ciphertext.append((char) ('A' + (A * (ch - 'A') + B) % 26));
            } else {
               ciphertext.append((char) ('a' + (A * (ch - 'a') + B) % 26));
            }
         } else {
            ciphertext.append(ch);
         }
      }
      return ciphertext.toString();
   }
    
   // Function to decrypt ciphertext
   static String decryptMessage(String ciphertext) {
      StringBuilder pt = new StringBuilder();
      int aInverse = modInverse(A, 26);
      if (aInverse == -1) {
         return "Inverse doesn't exist";
      }
      for (int i = 0; i < ciphertext.length(); i++) {
         char ch = ciphertext.charAt(i);
         if (Character.isLetter(ch)) {
            if (Character.isUpperCase(ch)) {
               int x = (aInverse * (ch - 'A' - B + 26)) % 26;
               pt.append((char) ('A' + x));
            } else {
               int x = (aInverse * (ch - 'a' - B + 26)) % 26;
               pt.append((char) ('a' + x));
            }
         } else {
            pt.append(ch);
         }
      }
      return pt.toString();
   }
    
   public static void main(String[] args) {
      String pt = "Hello this is an example of affine cipher";

      String et = encryptMessage(pt); // Encrypted Text
      System.out.println("The Encrypted Text: " + et);

      String dt = decryptMessage(et); // Decrypted Text
      System.out.println("The Decrypted Text: " + dt);
   }
}

以下是上述示例的输出：

输入/输出

The Encrypted Text: Jkzzy fjao ao uh kvuqpzk yb ubbahk capjkx
The Decrypted Text: Hello this is an example of affine cipher

使用C++的实现

我们将使用C++编程语言来实现仿射密码，这是一种保持消息秘密的方法。因此，这段代码的概念与我们在Java实现中使用的一样，但区别在于我们将在这里使用C++。

示例

因此，下面给出了C++中仿射密码的实现：

#include <iostream>
#include <string>
using namespace std;

const int A = 17; // Multiplicative Key
const int B = 20; // Additive Key

// function to find mod inverse
int modInverse(int a, int m) {
   for (int x = 1; x < m; x++) {
      if (((a % m) * (x % m)) % m == 1) {
         return x;
      }
   }
   return -1; // If inverse is not there
}

// Function to encrypt plaintext
string encryptMessage(string plaintext) {
   string ciphertext = "";
   for (char ch : plaintext) {
      if (isalpha(ch)) {
         if (isupper(ch)) {
            ciphertext += (char)('A' + (A * (ch - 'A') + B) % 26);
         } else {
            ciphertext += (char)('a' + (A * (ch - 'a') + B) % 26);
         }
      } else {
         ciphertext += ch;
      }
   }
   return ciphertext;
}

// Function to decrypt ciphertext
string decryptMessage(string ciphertext) {
   string plaintext = "";
   int aInverse = modInverse(A, 26);
   if (aInverse == -1) {
      return "Inverse doesn't exist";
   }
   for (char ch : ciphertext) {
      if (isalpha(ch)) {
         if (isupper(ch)) {
            int x = (aInverse * (ch - 'A' - B + 26)) % 26;
            plaintext += (char)('A' + x);
         } else {
            int x = (aInverse * (ch - 'a' - B + 26)) % 26;
            plaintext += (char)('a' + x);
         }
      } else {
         plaintext += ch;
      }
   }
   return plaintext;
}

int main() {
   string pt = "Hello there i am working with Affine Cipher";
   string et = encryptMessage(pt);
   cout << "Encrypted Text: " << et << endl;

   string dt = decryptMessage(et);
   cout << "Decrypted Text: " << dt << endl;

   return 0;
}

以下是上述示例的输出：

输入/输出

The Encrypted Text: Jkzzy fjkxk a uq eyxiahs eafj Ubbahk Capjkx
The Decrypted Text: Hello there i am working with Affine Cipher

特点

  • 易于理解和实现。

  • 字母表的大小可以调整。

  • 它允许使用不同的密钥进行加密和解密。因此，它在选择安全级别方面提供了灵活性。

  • 加密和解密过程包括数值运算，这为编码的消息增加了一层安全性。

缺点

  • 可能的密钥数量受字母集大小的限制，这容易受到暴力攻击。

  • 由于仿射密码保留了字母频率，因此它容易受到频率分析攻击。

  • 它只关注加密和解密，缺乏数据完整性验证或发送者身份验证机制。

总结

在本章中，我们学习了仿射密码算法，用于加密和解密我们的秘密信息。它使用数学公式来加密和解密给定的消息。它有助于保护消息安全，方法是将它们转换成只有使用正确的数字才能理解的秘密代码。我们还看到了使用Python以不同方式实现仿射密码的方法。一种方法涉及使用模算术运算，我们在其中将数字保持在特定范围内。另一种方法使用字典映射，其中每个字母根据公式替换为其加密或解密版本。

打印页面
上一页
下一页
广告