密码学 - 电子密码本 (ECB) 模式

电子密码本 (ECB) 是一种基本的分组密码操作模式，主要与对称密钥加密一起使用。它是一种处理按顺序排列的消息块列表的简单方法。

输入明文中包含多个块。加密密钥用于独立且单独地加密每个块（密文）。因此，也可以单独解密每个加密块。每种块都可以由 ECB 支持的不同加密密钥。

ECB 中的每个明文块都有一个预定义的密文值与之匹配，反之亦然。因此，使用相同的密钥，总是可以从相同的明文加密得到相同的密文。这意味着如果明文块 P1、P2 等使用相同的密钥多次加密，输出的密文块将始终相同。

换句话说，密文值将始终等于明文值。这对于包含某些相同部分的明文也成立。例如，具有相同字母标题并使用相同密钥加密的明文将包含很大程度上相同的密文部分。

操作

• 要创建第一个密文块，用户取第一个明文块并使用密钥对其进行加密。

• 然后，他使用相同的过程和密钥处理第二个明文块，依此类推。

由于 ECB 模式是确定性的，如果明文块 P1、P2……和 Pm 使用相同的密钥两次加密，则生成的密文块将相同。

实际上，我们可以为给定密钥的每个可能的明文块技术上生成一个密文代码本。然后，加密只需要查找必要的明文并选择相应的密文即可。因此，此过程类似于在密码本中分配代码字，这就是它拥有官方名称的原因：电子密码本操作模式 (ECB)。以下是它的可视化表示 -

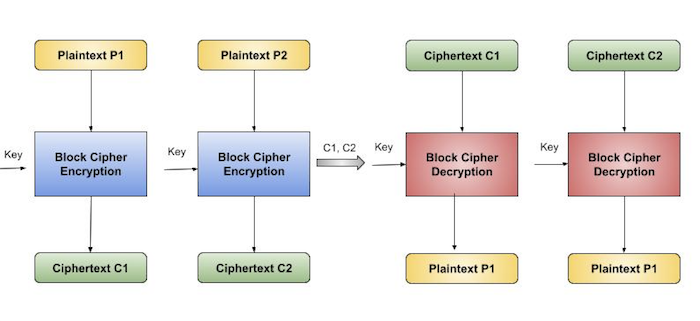
ECB 模式的分析

在现实生活中，应用程序数据通常包含可猜测的部分信息。例如，可以推断出薪资范围。如果明文消息包含在可预测的区域中，攻击者可以通过反复试验从 ECB 中解密密文。

例如，如果薪资数字使用 ECB 模式的密文加密，攻击者可以在有限次数的尝试后检索到薪资数字。由于大多数应用程序都不希望使用确定性密码，因此不应在其中使用 ECB 模式。

数据加密标准与电子密码本

IBM 在 1970 年代初期创建了数据加密标准 (DES)，并在 1977 年被认可为联邦信息处理标准 (FIPS)。DES 可以通过五种不同的方式加密数据。其中包括原始 DES 模式或 ECB。

FIPS 版本 81 现在包含三个新选项：密码分组链接 (CBC)、密码反馈 (CFB) 和输出反馈 (OFB)。后来，NIST 特别出版物 800-38a 更新为包含第五种模式，称为计数器模式。这些模式的设计理念各不相同，包括是否使用初始化向量，是否使用块而不是流，以及加密错误是否可能传播到后续块。

使用 Python 实现

此实现使用简单的字节级操作执行 ECB 加密和解密。务必记住，在大多数情况下，ECB 模式不安全，需要替换为更安全的模式，如 CBC 或 GCM。

以下是 ECB 模式加密和解密的简单 Python 实现 -

示例

# ECB encryption & decryption
def pad(text, block_size):
   padding_length = block_size - (len(text) % block_size)
   padding = bytes([padding_length] * padding_length)
   return text + padding

def unpad(padded_text):
   padding_length = padded_text[-1]
   return padded_text[:-padding_length]

def xor_bytes(byte1, byte2):
   return bytes([a ^ b for a, b in zip(byte1, byte2)])
#Encryption Method
def encrypt_ecb(key, plaintext):
   block_size = len(key)
   padded_plaintext = pad(plaintext, block_size)
   num_blocks = len(padded_plaintext) // block_size

   cipher_text = b''
   for i in range(num_blocks):
      block_start = i * block_size
      block_end = block_start + block_size
      block = padded_plaintext[block_start:block_end]

      encrypted_block = xor_bytes(block, key)
      cipher_text += encrypted_block

   return cipher_text
# Decryption Method
def decrypt_ecb(key, ciphertext):
   block_size = len(key)
   num_blocks = len(ciphertext) // block_size

   plain_text = b''
   for i in range(num_blocks):
      block_start = i * block_size
      block_end = block_start + block_size
      block = ciphertext[block_start:block_end]

      decrypted_block = xor_bytes(block, key)
      plain_text += decrypted_block

   return unpad(plain_text)

# key and plaintext
key = b'ABCDEFGHIJKLMNOP'  # 16 bytes key for AES-128
plaintext = b'Hello, Tutorialspoint!'
ciphertext = encrypt_ecb(key, plaintext)
print("Ciphertext:", ciphertext)
decrypted_plaintext = decrypt_ecb(key, ciphertext)
print("Decrypted plaintext:", decrypted_plaintext.decode('utf-8'))

输出

Ciphertext: b"\t'/(*jg\x1c<>$>$/##1-**1gMBC@AFGDEZ"
Decrypted plaintext: Hello, Tutorialspoint!

ECB 模式的缺点

以下是使用 ECB 模式的一些缺点 -

• ECB 不使用链接或初始化向量；而是使用基本的替换。由于这些特性，它易于实现。但这也是其最大的弱点。由于两个相同的明文块提供两个完全相同的密文块，因此它在密码学上很弱。

• 当使用相同的加密模式和小块大小（小于 40 位）时，不推荐使用 ECB。当块大小较小时，明文中可能会出现一些单词和短语。这也意味着可能会出现相同的重复部分密文块，并且密文可以携带来自相同明文的模式。当明文模式易于识别时，黑客更有可能发现它们并执行代码本攻击。

• 即使 ECB 安全性不足，也可以通过添加每个块的随机填充位来改进它。较大的块（64 位或更多）可能具有足够的熵或特殊特性来防止代码本攻击。