公钥加密

上一个
下一个

公钥加密

与对称密钥加密不同，我们没有发现公钥加密的历史应用。这是一个相对较新的概念。

对称加密非常适合政府、军事和大型金融公司等组织，这些组织参与了机密通信。

在过去几十年中，随着越来越多的不安全的计算机网络的普及，人们真正感受到了大规模使用加密的需求。由于对称密钥在密钥管理方面面临的挑战，发现它不切实际。这催生了公钥密码系统。

加密和解密的过程在下面的插图中描述：

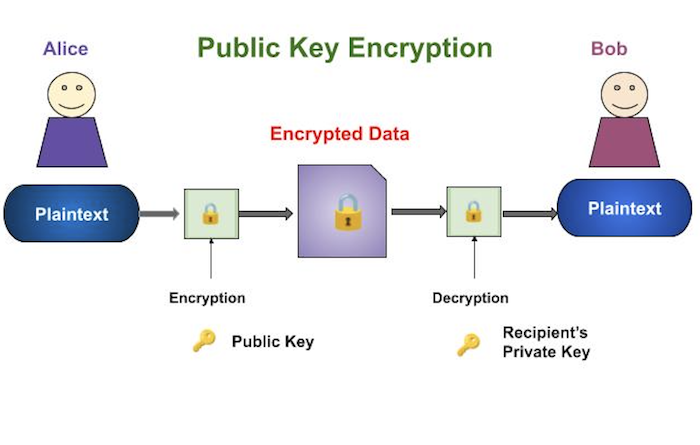
Public Key Cryptography

公钥加密方案最重要的属性是：

  • 加密和解密使用不同的密钥。这是使该方案与对称加密方案不同的属性。

  • 每个接收者都拥有一个唯一的解密密钥，通常称为其私钥。

  • 接收者需要发布一个加密密钥，称为其公钥。

  • 此方案需要确保公钥的真实性，以避免对手冒充接收者。通常，这种类型的密码系统涉及可信的第三方，该第三方证明特定的公钥仅属于特定的人或实体。

  • 加密算法足够复杂，可以禁止攻击者根据密文和加密（公钥）推断明文。

  • 尽管私钥和公钥在数学上相关，但从公钥计算私钥是不可行的。事实上，任何公钥密码系统中的智能部分都在于设计两个密钥之间的关系。

公钥加密方案有三种类型。我们在以下部分讨论它们：

RSA 密码系统

该密码系统是最初的系统之一。即使在今天，它仍然是最常用的密码系统。该系统由三位学者罗恩·莱维斯特、阿迪·萨莫尔和伦纳德·阿德曼发明，因此被称为 RSA 密码系统。

我们将看到 RSA 密码系统的两个方面，首先是密钥对的生成，其次是加密解密算法。

RSA 密钥对的生成

每个希望使用加密参与通信的人或一方都需要生成一对密钥，即公钥和私钥。密钥生成过程中遵循的过程如下所述：

  • 生成 RSA 模数 (n)

    • 选择两个大素数 p 和 q。

    • 计算 n=p*q。对于强大的不可破解加密，让 n 为一个大数，通常至少为 512 位。

  • 查找导出数字 (e)

    • 数字e必须大于 1 且小于 (p − 1)(q − 1)。

    • e 和 (p − 1)(q − 1) 之间除了 1 之外没有公因子。换句话说，两个数字 e 和 (p – 1)(q – 1) 是互质的。

  • 形成公钥

    • 数字对 (n, e) 形成 RSA 公钥，并公开。

    • 有趣的是，虽然 n 是公钥的一部分，但难以对大素数进行因式分解确保攻击者无法在有限时间内找到用于获得 n 的两个素数 (p & q)。这是 RSA 的优势。

  • 生成私钥

    • 私钥 d 由 p、q 和 e 计算得出。对于给定的 n 和 e，存在唯一的数字 d。

    • 数字 d 是 e 模 (p - 1)(q – 1) 的逆。这意味着 d 是小于 (p - 1)(q - 1) 的数字，当乘以 e 时，它等于 1 模 (p - 1)(q - 1)。

    • 这种关系用数学表示如下：

ed = 1 mod (p − 1)(q − 1)

扩展欧几里得算法以 p、q 和 e 作为输入，并以 d 作为输出。

示例

下面给出了生成 RSA 密钥对的示例。（为了便于理解，这里取的素数 p & q 是小值。实际上，这些值非常高）。

  • 令两个素数为 p = 7 和 q = 13。因此，模数 n = pq = 7 x 13 = 91。

  • 选择 e = 5，这是一个有效的选择，因为除了 1 之外，5 和 (p − 1)(q − 1) = 6 × 12 = 72 没有公因子。

  • 数字对 (n, e) = (91, 5) 形成公钥，可以提供给任何我们希望能够向我们发送加密消息的人。

  • 将 p = 7、q = 13 和 e = 5 输入扩展欧几里得算法。输出将为 d = 29。

  • 通过计算检查计算出的 d 是否正确：

de = 29 × 5 = 145 = 1 mod 72

  • 因此，公钥为 (91, 5)，私钥为 (91, 29)。

加密和解密

密钥对生成后，加密和解密过程相对简单且计算量少。

有趣的是，RSA 不像对称密钥加密那样直接对位串进行操作。它对模 n 的数字进行操作。因此，有必要将明文表示为一系列小于 n 的数字。

RSA 加密

  • 假设发送方希望向某个人的公钥为 (n, e) 的人发送一些文本消息。

  • 然后，发送方将明文表示为一系列小于 n 的数字。

  • 要加密第一个明文 P，它是模 n 的一个数字。加密过程是一个简单的数学步骤，如下所示：

C = Pe mod n

  • 换句话说，密文 C 等于明文 P 自乘 e 次，然后模 n。这意味着 C 也是小于 n 的数字。

  • 回到我们的密钥生成示例，明文 P = 10，我们得到密文 C：

C = 105 mod 91

RSA 解密

  • RSA 的解密过程也非常简单。假设公钥对 (n, e) 的接收者已收到密文 C。

  • 接收者将 C 提升到其私钥 d 的幂。模 n 的结果将是明文 P。

Plaintext = Cd mod n

  • 再次回到我们的数值示例，密文 C = 82 将使用私钥 29 解密为数字 10：

Plaintext = 8229 mod 91 = 10

RSA 分析

RSA 的安全性取决于两个独立函数的强度。RSA 密码系统是最流行的公钥密码系统，其强度基于对非常大的数字进行因式分解的实际困难。

  • 加密函数 - 它被认为是一个将明文转换为密文的单向函数，只有知道私钥d才能将其逆转。

  • 密钥生成 - 从RSA公钥确定私钥的难度等同于对模数n进行因式分解。因此，攻击者无法利用RSA公钥的知识来确定RSA私钥，除非他能对n进行因式分解。它也是一个单向函数，从p和q值到模数n很容易，但反过来就不可能了。

如果这两个函数中的任何一个被证明不是单向的，那么RSA就会被破解。事实上，如果开发出一种有效的因式分解技术，那么RSA将不再安全。

如果数字p和q不是大素数，和/或选择的公钥e是一个小数字，那么RSA加密的强度会大幅下降，容易受到攻击。

ElGamal密码系统

除了RSA之外，还有其他提出的公钥密码系统。它们中的许多都基于离散对数问题的不同版本。

ElGamal密码系统，称为椭圆曲线变体，基于离散对数问题。它的强度源于这样一个假设，即对于给定的数字，在实际时间范围内无法找到离散对数，而幂运算的反运算可以有效地计算。

让我们来看一下ElGamal的一个简单版本，它使用模p的数字。在椭圆曲线变体的情况下，它是基于完全不同的数字系统。

ElGamal密钥对生成

ElGamal密码系统的每个用户都通过以下方式生成密钥对：

  • 选择一个大素数p。通常选择一个长度为1024到2048位的素数。

  • 选择一个生成元g。

    • 这个数字必须在1和p-1之间，但不能是任意数字。

    • 它是模p整数乘法群的生成元。这意味着对于每个与p互质的整数m，都存在一个整数k，使得gk=a mod n。

      例如，3是群5（Z5 = {1, 2, 3, 4}）的生成元。

N 3n 3n mod 5
1 3 3
2 9 4
3 27 2
4 81 1

  • 选择私钥。私钥x是任何大于1且小于p-1的数字。

  • 计算公钥的一部分。值y根据参数p、g和私钥x计算如下：

y = gx mod p

  • 获取公钥。ElGamal公钥由三个参数（p、g、y）组成。

    例如，假设p = 17且g = 6（可以确认6是群Z17的生成元）。私钥x可以是大于1且小于71的任何数字，因此我们选择x = 5。然后计算值y如下：

y = 65 mod 17 = 7

  • 因此私钥是62，公钥是（17，6，7）。

加密和解密

与RSA等效的过程相比，ElGamal密钥对的生成相对简单。但加密和解密比RSA稍微复杂一些。

ElGamal加密

假设发送方希望将明文发送给某人，其ElGamal公钥为（p、g、y），则：

  • 发送方将明文表示为一系列模p的数字。

  • 要加密表示为模p数字的第一个明文P。获取密文C的加密过程如下：

    • 随机生成一个数字k；
    • 计算两个值C1和C2，其中：
C1 = gk mod p
C2 = (P*yk) mod p

  • 将密文C发送，密文C由两个单独的值（C1，C2）组成，一起发送。

  • 参考上面给出的ElGamal密钥生成示例，明文P = 13加密如下：

    • 随机生成一个数字，比如k = 10
    • 计算两个值C1和C2，其中：
C1 = 610 mod 17
C2 = (13*710) mod 17 = 9

  • 发送密文C = (C1，C2) = (15，9)。

ElGamal解密

  • 要使用私钥x解密密文（C1，C2），需要执行以下两个步骤：

    • 计算(C1)x模p的模逆，即(C1)-x，通常称为解密因子。

    • 使用以下公式获取明文：

C2 × (C1)-x  mod p = Plaintext

  • 在我们的示例中，要使用私钥x = 5解密密文C = (C1，C2) = (15，9)，解密因子为

15-5  mod 17 = 9

  • 提取明文P = (9 × 9) mod 17 = 13。

ElGamal分析

在ElGamal系统中，每个用户都有一个私钥x，并且有三个组成部分的公钥：素模p、生成元g和公钥Y = gx mod p。ElGamal的强度基于离散对数问题的难度。

安全密钥大小通常> 1024位。如今甚至使用2048位长的密钥。在处理速度方面，Elgamal相当慢，它主要用于密钥认证协议。由于更高的处理效率，ElGamal的椭圆曲线变体正变得越来越受欢迎。

椭圆曲线密码学（ECC）

椭圆曲线密码学（ECC）是一个术语，用于描述一套密码工具和协议，其安全性基于离散对数问题的特殊版本。它不使用模p的数字。

ECC基于与称为椭圆曲线的数学对象相关联的一组数字。这些数字有加法和计算倍数的规则，就像模p的数字一样。

ECC包含许多最初为模数设计的密码方案的变体，例如ElGamal加密和数字签名算法。

人们认为，当应用于椭圆曲线上的点时，离散对数问题要困难得多。这促使我们从模p的数字切换到椭圆曲线上的点。此外，如果我们使用基于椭圆曲线的变体，则可以使用更短的密钥获得等效的安全级别。

更短的密钥带来两个好处：

  • 密钥管理简便
  • 计算效率高

这些优势使基于椭圆曲线的加密方案变体对于计算资源受限的应用极具吸引力。

RSA和ElGamal方案 - 对比

让我们简要比较一下RSA和ElGamal方案在各个方面的差异。

RSA ElGamal
它在加密方面效率更高。 它在解密方面效率更高。
它在解密方面效率较低。 它在解密方面效率更高。
对于特定的安全级别，RSA需要较长的密钥。 对于相同的安全级别，需要非常短的密钥。
它被广泛接受和使用。 它比较新，在市场上并不流行。
打印页面
上一页
下一页
广告