Boyer-Moore 算法

上一页
下一页

用于模式匹配的Boyer-Moore算法

Boyer-Moore算法用于确定给定模式是否存在于指定文本中。它采用了一种反向的模式搜索/匹配方法。在一个给定字符串中搜索特定模式的任务被称为模式搜索问题。例如，如果文本是“THIS IS A SAMPLE TEXT”，模式是“TEXT”，则输出应为10，这是模式在给定文本中第一次出现的索引。

该算法由Robert Boyer和J Strother Moore于1977年开发。它被认为是最有效和最广泛使用的模式匹配算法。

Boyer-Moore算法是如何工作的？

在前面的章节中，我们已经看到了解决这个问题的简单方法，它涉及到逐个滑动模式覆盖文本，并比较每个字符。然而，这种方法非常慢，因为它需要O(n*m)时间，其中'n'是文本的长度，'m'是模式的长度。Boyer-Moore算法通过预处理模式并使用两种启发式方法来跳过一些不可能匹配的比较来改进这一点。

这两种启发式方法如下：

  • 坏字符启发式 - 此启发式方法使用一个表来存储模式中每个字符的最后出现位置。当文本中某个字符（坏字符）发生不匹配时，算法会检查此字符是否出现在模式中。如果出现，则它会移动模式，使模式中该字符的最后出现位置与文本中的坏字符对齐。如果没有，则它会将模式移过坏字符。

  • 好后缀启发式 - 此启发式方法使用另一个表来存储当坏字符启发式方法失败时的移位信息。在这种情况下，我们会在模式内查找，直到坏字符变成文本的好后缀。然后我们继续移动以查找给定的模式。

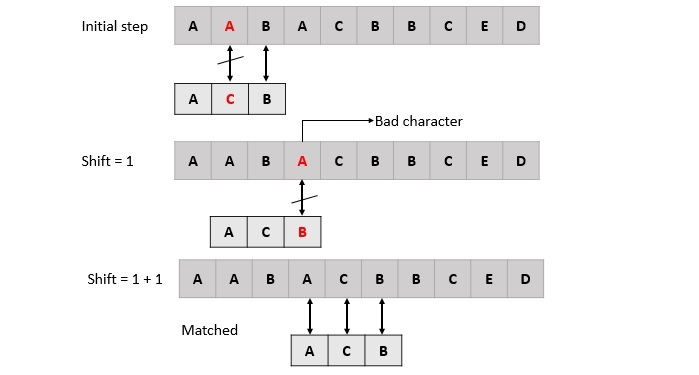
Boyer Solution

Boyer-Moore算法通过在每一步选择它们建议的最大位移来组合这两种启发式方法。在这个过程中，子串或模式是从模式的最后一个字符开始搜索的。当主字符串的子串与模式的子串匹配时，它会移动以查找匹配子串的其他出现位置。如果发生不匹配，它会应用启发式方法并相应地移动模式。当找到完全匹配或到达文本末尾时，算法停止。

Boyer-Moore算法的最坏情况时间复杂度为O(nm)，但是，它的性能可能远高于此。事实上，在某些情况下，它可以达到O(n/m)的亚线性时间复杂度，这意味着它可以在不比较文本中某些字符的情况下跳过这些字符。当模式没有重复字符或具有较大的字母表大小时，就会发生这种情况。

为了说明Boyer-Moore算法是如何工作的，让我们考虑一个例子：

Input:
main String: "AABAAABCEDBABCDDEBC" 
pattern: "ABC"
Output:
Pattern found at position: 5
Pattern found at position: 11

示例

在下面的示例中，我们将演示Boyer-Moore算法在各种编程语言中的工作方式。

C语言 C++ Java Python
#include<stdio.h> 
#include<string.h> 
// Function for full suffix match
void computeFullShift(int shiftArr[], int longSuffArr[], char patrn[], int n) {
   int i = n;
   int j = n+1;
   longSuffArr[i] = j;
   while(i > 0) {
      // Searching right if (i-1)th and (j-1)th item are not the same
      while(j <= n && patrn[i-1] != patrn[j-1] ) {
          // to shift pattern from i to j
         if(shiftArr[j] == 0) {
            shiftArr[j] = j-i; 
         }
         // Updating long suffix value
         j = longSuffArr[j]; 
      }
      i--;
      j--;
      longSuffArr[i] = j;
   }  
}
// Function for good suffix match
void computeGoodSuffix(int shiftArr[], int longSuffArr[], char patrn[], int n) {
   int j;
   j = longSuffArr[0];
   // Looping through the pattern
   for(int i = 0; i<n; i++) {
      // setting shift to long suffix value
      if(shiftArr[i] == 0) {
         shiftArr[i] = j; 
         if(i == j) {
            // Updating long suffix value
            j = longSuffArr[j]; 
         }
      }
   }
}
// Function for searching the pattern
void searchPattern(char orgnStr[], char patrn[], int array[], int *index) {
   // length of the pattern
   int patLen = strlen(patrn); 
   // length of main string
   int strLen = strlen(orgnStr);
   int longerSuffArray[patLen+1];
   int shiftArr[patLen + 1];
   // Initializing shift array elements to 0
   for(int i = 0; i<=patLen; i++) {
      shiftArr[i] = 0;
   }
   // Calling computeFullShift function
   computeFullShift(shiftArr, longerSuffArray, patrn, patLen); 
   // Calling computeGoodSuffix function
   computeGoodSuffix(shiftArr, longerSuffArray, patrn, patLen); 
   int shift = 0;
   while(shift <= (strLen - patLen)) {
      int j = patLen - 1;
      // decrement j when pattern and main string character is matching
      while(j >= 0 && patrn[j] == orgnStr[shift+j]) {
         j--; 
      }
      if(j < 0) {
         (*index)++;
         // to store the position where pattern is found
         array[(*index)] = shift; 
         shift += shiftArr[0];
      }else {
          shift += shiftArr[j+1];
      }
   }
}
int main() {
   // original string    
   char orgnStr[] = "AABAAABCEDBABCDDEBC"; 
   // Pattern to be searched
   char patrn[] = "ABC"; 
   // Array to store the positions where pattern is found
   int locArray[strlen(orgnStr)]; 
   int index = -1;
   // Calling the searchPattern function
   searchPattern(orgnStr, patrn, locArray, &index); 
   // Printing the positions where pattern is found
   for(int i = 0; i <= index; i++) {
      printf("Pattern found at position: %d\n", locArray[i]);
   }
   return 0;
}

#include<iostream> 
using namespace std; 
// Function for full suffix match
void computeFullShift(int shiftArr[], int longSuffArr[], string patrn) {
   // length of pattern
   int n = patrn.size(); 
   int i = n;
   int j = n+1;
   longSuffArr[i] = j;
   while(i > 0) {
      // Searching right if (i-1)th and (j-1)th item are not the same
      while(j <= n && patrn[i-1] != patrn[j-1] ) {
          // to shift pattern from i to j
         if(shiftArr[j] == 0) {
            shiftArr[j] = j-i; 
         }
         // Updating long suffix value
         j = longSuffArr[j]; 
      }
      i--;
      j--;
      longSuffArr[i] = j;
   }  
}
// Function for good suffix match
void computeGoodSuffix(int shiftArr[], int longSuffArr[], string patrn) {
   // length of the pattern
   int n = patrn.size(); 
   int j;
   j = longSuffArr[0];
   // Looping through the pattern
   for(int i = 0; i<n; i++) {
      // setting shift to long suffix value
      if(shiftArr[i] == 0) {
         shiftArr[i] = j; 
         if(i == j) {
            // Updating long suffix value
            j = longSuffArr[j]; 
         }
      }
   }
}
// Function for searching the pattern
void searchPattern(string orgnStr, string patrn, int array[], int *index) {
   // length of the pattern
   int patLen = patrn.size(); 
   // length of main string
   int strLen = orgnStr.size();
   int longerSuffArray[patLen+1];
   int shiftArr[patLen + 1];
   // Initializing shift array elements to 0
   for(int i = 0; i<=patLen; i++) {
      shiftArr[i] = 0;
   }
   // Calling computeFullShift function
   computeFullShift(shiftArr, longerSuffArray, patrn); 
   // Calling computeGoodSuffix function
   computeGoodSuffix(shiftArr, longerSuffArray, patrn); 
   int shift = 0;
   while(shift <= (strLen - patLen)) {
      int j = patLen - 1;
      // decrement j when pattern and main string character is matching
      while(j >= 0 && patrn[j] == orgnStr[shift+j]) {
         j--; 
      }
      if(j < 0) {
         (*index)++;
         // to store the position where pattern is found
         array[(*index)] = shift; 
         shift += shiftArr[0];
      }else {
          shift += shiftArr[j+1];
      }
   }
}
int main() {
   // original string    
   string orgnStr = "AABAAABCEDBABCDDEBC"; 
   // Pattern to be searched
   string patrn = "ABC"; 
   // Array to store the positions where pattern is found
   int locArray[orgnStr.size()]; 
   int index = -1;
   // Calling the searchPattern function
   searchPattern(orgnStr, patrn, locArray, &index); 
   // Printing the positions where pattern is found
   for(int i = 0; i <= index; i++) {
      cout << "Pattern found at position: " << locArray[i]<<endl;
   }
}

public class BMalgo {
   // method for full suffix match
   static void computeFullShift(int[] shiftArr, int[] longSuffArr, String patrn) {
      // length of pattern
      int n = patrn.length();
      int i = n;
      int j = n+1;
      longSuffArr[i] = j;
      while(i > 0) {
         // Searching right if (i-1)th and (j-1)th item are not the same
         while(j <= n && patrn.charAt(i-1) != patrn.charAt(j-1)) {
            // to shift pattern from i to j
            if(shiftArr[j] == 0) {
               shiftArr[j] = j-i;
            }
            // Updating long suffix value
            j = longSuffArr[j];
         }
         i--;
         j--;
         longSuffArr[i] = j;
      }
   }
   // method for good suffix match
   static void computeGoodSuffix(int[] shiftArr, int[] longSuffArr, String patrn) {
      // length of the pattern
      int n = patrn.length();
      int j;
      j = longSuffArr[0];
      // Looping through the pattern
      for(int i = 0; i<n; i++) {
         // setting shift to long suffix value
         if(shiftArr[i] == 0) {
            shiftArr[i] = j;
            if(i == j) {
               // Updating long suffix value
               j = longSuffArr[j];
            }
         }
      }
   }
   // method for searching the pattern
   static void searchPattern(String orgnStr, String patrn, int[] array, int[] index) {
      // length of the pattern
      int patLen = patrn.length();
      // length of main string
      int strLen = orgnStr.length();
      int[] longerSuffArray = new int[patLen+1];
      int[] shiftArr = new int[patLen + 1];
      // Initializing shift array elements to 0
      for(int i = 0; i<=patLen; i++) {
         shiftArr[i] = 0;
      }
      // Calling computeFullShift method
      computeFullShift(shiftArr, longerSuffArray, patrn);
      // Calling computeGoodSuffix method
      computeGoodSuffix(shiftArr, longerSuffArray, patrn);
      int shift = 0;
      while(shift <= (strLen - patLen)) {
         int j = patLen - 1;
         // decrement j when pattern and main string character is matching
         while(j >= 0 && patrn.charAt(j) == orgnStr.charAt(shift+j)) {
            j--;
         }
         if(j < 0) {
            index[0]++;
            // to store the position where pattern is found
            array[index[0]] = shift;
            shift += shiftArr[0];
         }else {
            shift += shiftArr[j+1];
         }
      }
   }
   public static void main(String[] args) {
      // original string
      String orgnStr = "AABAAABCEDBABCDDEBC";
      // Pattern to be searched
      String patrn = "ABC";
      // Array to store the positions where pattern is found
      int[] locArray = new int[orgnStr.length()];
      int[] index = {-1};
      // Calling the searchPattern method
      searchPattern(orgnStr, patrn, locArray, index);
      // Printing the positions where pattern is found
      for(int i = 0; i <= index[0]; i++) {
         System.out.println("Pattern found at position: " + locArray[i]);
      }
   }
}

# Function for full suffix match
def compute_full_shift(shift_arr, long_suff_arr, patrn):
    # length of pattern
    n = len(patrn)
    i = n
    j = n+1
    long_suff_arr[i] = j
    while i > 0:
        # Searching right if (i-1)th and (j-1)th item are not the same
        while j <= n and patrn[i-1] != patrn[j-1]:
            # to shift pattern from i to j
            if shift_arr[j] == 0:
                shift_arr[j] = j-i
            # Updating long suffix value
            j = long_suff_arr[j]
        i -= 1
        j -= 1
        long_suff_arr[i] = j
# Function for good suffix match
def compute_good_suffix(shift_arr, long_suff_arr, patrn):
    # length of the pattern
    n = len(patrn)
    j = long_suff_arr[0]
    # Looping through the pattern
    for i in range(n):
        # setting shift to long suffix value
        if shift_arr[i] == 0:
            shift_arr[i] = j
            if i == j:
                # Updating long suffix value
                j = long_suff_arr[j]

# Function for searching the pattern
def search_pattern(orgn_str, patrn, array, index):
    # length of the pattern
    pat_len = len(patrn)
    # length of main string
    str_len = len(orgn_str)
    longer_suff_array = [0]*(pat_len+1)
    shift_arr = [0]*(pat_len + 1)
    # Initializing shift array elements to 0
    for i in range(pat_len+1):
        shift_arr[i] = 0
    # Calling compute_full_shift function
    compute_full_shift(shift_arr, longer_suff_array, patrn)
    # Calling compute_good_suffix function
    compute_good_suffix(shift_arr, longer_suff_array, patrn)
    shift = 0
    while shift <= (str_len - pat_len):
        j = pat_len - 1
        # decrement j when pattern and main string character is matching
        while j >= 0 and patrn[j] == orgn_str[shift+j]:
            j -= 1
        if j < 0:
            index[0] += 1
            # to store the position where pattern is found
            array[index[0]] = shift
            shift += shift_arr[0]
        else:
            shift += shift_arr[j+1]

# original string
orgn_str = "AABAAABCEDBABCDDEBC"
# Pattern to be searched
patrn = "ABC"
# Array to store the positions where pattern is found
loc_array = [0]*len(orgn_str)
index = [-1]
# Calling the search_pattern function
search_pattern(orgn_str, patrn, loc_array, index)
# Printing the positions where pattern is found
for i in range(index[0]+1):
    print("Pattern found at position: ", loc_array[i])

输出

Pattern found at position: 5
Pattern found at position: 11
打印页面
上一页
下一页
广告