骑士巡游问题

上一页
下一页

什么是骑士巡游问题？

在骑士巡游问题中，我们得到一个大小为NxN的空棋盘和一个骑士。在国际象棋中，骑士是一个看起来像马的棋子。假设它可以从棋盘上的任何位置开始。现在，我们的任务是检查骑士是否可以访问棋盘上的所有方格。当它可以访问所有方格时，打印从起始位置到达该位置所需的跳跃次数。

骑士可以有两种方式完成它的巡游。在第一种方式中，骑士移动一步并返回到起始位置形成一个循环，这称为闭合巡游。在第二种方式即开放巡游中，它在棋盘上的任何位置结束。

对于不熟悉国际象棋的人，请注意骑士的移动方式很特殊。它可以在每个方向上水平移动两个方格和垂直移动一个方格，或者垂直移动两个方格和水平移动一个方格。因此，完整的移动看起来像英文字母'L'。

Knight's Move

假设给定棋盘的大小为8，并且骑士位于棋盘的左上角位置。接下来的可能的移动如下所示：

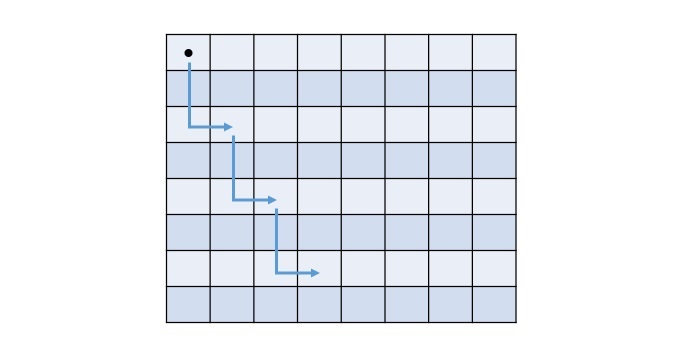
Knight's Solution

上面棋盘中的每个单元格都包含一个数字，表示从哪里开始以及骑士需要多少步才能到达一个单元格。单元格的最终值将由以下矩阵表示：

  0  59  38  33  30  17   8  63 
 37  34  31  60   9  62  29  16 
 58   1  36  39  32  27  18   7 
 35  48  41  26  61  10  15  28 
 42  57   2  49  40  23   6  19 
 47  50  45  54  25  20  11  14 
 56  43  52   3  22  13  24   5 
 51  46  55  44  53   4  21  12

请记住，此问题可能有多个解决方案，上面的矩阵是一个可能的解决方案。

解决骑士巡游问题的一种方法是逐一生成所有巡游，然后检查它们是否满足指定的约束条件。但是，这很耗时，不是一种有效的方法。

回溯法解决骑士巡游问题

解决此问题的另一种方法是使用回溯法。这是一种尝试不同可能性直到找到解决方案或尝试所有选项的技术。它包括选择一个移动，执行它，然后递归地尝试解决问题的其余部分。如果当前移动导致死胡同，我们回溯并撤消该移动，然后尝试另一个移动。

要使用回溯法解决骑士巡游问题，请按照以下步骤操作：

  • 从棋盘上的任何一个单元格开始，并将其标记为骑士已访问。

  • 将骑士移动到一个有效的未访问单元格，并将其标记为已访问。从任何一个单元格，骑士最多可以进行8次移动。

  • 如果当前单元格无效或没有通往解决方案的路径，则回溯并尝试其他可能通往解决方案的移动。

  • 重复此过程，直到骑士的移动次数等于8 x 8 = 64。

示例

在下面的示例中，我们将实际演示如何解决骑士巡游问题。

C C++ Java Python
#include <stdio.h>
#define N 8
int sol[N][N];
//check place is in range and not assigned yet
int isValid(int x, int y) {    
   return ( x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1);
}
void displaySolution() {
   printf("The possible solution: \n");    
   for (int x = 0; x < N; x++) {
      for (int y = 0; y < N; y++)
         printf("%3d ", sol[x][y]);
      printf("\n");
   }
}
int knightTour(int x, int y, int move, int xMove[N], int yMove[N]) {
   int xNext, yNext;
   //when the total board is covered
   if (move == N*N)     
      return 1;
   for (int k = 0; k < 8; k++) {
      xNext = x + xMove[k];
      yNext = y + yMove[k];
      //check room is preoccupied or not
      if (isValid(xNext, yNext)) {     
         sol[xNext][yNext] = move;
         if (knightTour(xNext, yNext, move+1, xMove, yMove) == 1)
            return 1;
         else
            // backtracking
            sol[xNext][yNext] = -1;
      }
   }
   return 0;
}
int findKnightTourSol() {
   //initially set all values to -1 of solution matrix    
   for (int x = 0; x < N; x++)     
      for (int y = 0; y < N; y++)
         sol[x][y] = -1;
   //all possible moves for knight
   int xMove[8] = {  2, 1, -1, -2, -2, -1,  1,  2 };
   int yMove[8] = {  1, 2,  2,  1, -1, -2, -2, -1 };
   //starting from room (0, 0)
   sol[0][0]  = 0;     
   if (knightTour(0, 0, 1, xMove, yMove) == 0) {
      printf("Solution does not exist");
      return 0;
   } else
      displaySolution();
   return 1;
}
int main() {
   findKnightTourSol();
   return 0;
}

#include <iostream>
#include <iomanip>
#define N 8
using namespace std;
int sol[N][N];
 //check place is in range and not assigned yet
bool isValid(int x, int y, int sol[N][N]) {    
   return ( x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1);
}
void displaySolution() {
   cout << "The possible solution: " << endl;    
   for (int x = 0; x < N; x++) {
      for (int y = 0; y < N; y++)
         cout << setw(3) << sol[x][y] << " ";
      cout << endl;
   }
}
int knightTour(int x, int y, int move, int sol[N][N], int xMove[N], int yMove[N]) {
   int xNext, yNext;
   //when the total board is covered
   if (move == N*N)     
      return true;
   for (int k = 0; k < 8; k++) {
      xNext = x + xMove[k];
      yNext = y + yMove[k];
      //check room is preoccupied or not
      if (isValid(xNext, yNext, sol)) {     
         sol[xNext][yNext] = move;
         if (knightTour(xNext, yNext, move+1, sol, xMove, yMove) == true)
            return true;
         else
            // backtracking
            sol[xNext][yNext] = -1;
      }
   }
   return false;
}
bool findKnightTourSol() {
   //initially set all values to -1 of solution matrix    
   for (int x = 0; x < N; x++)     
      for (int y = 0; y < N; y++)
         sol[x][y] = -1;
   //all possible moves for knight
   int xMove[8] = {  2, 1, -1, -2, -2, -1,  1,  2 };
   int yMove[8] = {  1, 2,  2,  1, -1, -2, -2, -1 };
   //starting from room (0, 0)
   sol[0][0]  = 0;     
   if (knightTour(0, 0, 1, sol, xMove, yMove) == false) {
      cout << "Solution does not exist";
      return false;
   } else
      displaySolution();
   return true;
}
int main() {
   findKnightTourSol();
}

import java.util.Arrays;
public class Main {
   static final int N = 8;
   static int[][] sol = new int[N][N];
   //check place is in range and not assigned yet
   static boolean isValid(int x, int y) {    
      return (x >= 0 && x < N && y >= 0 && y < N && sol[x][y] == -1);
   }
   static void displaySolution() {
      System.out.println("The possible solution: ");
      for (int x = 0; x < N; x++) {
         for (int y = 0; y < N; y++)
            System.out.printf("%3d ", sol[x][y]);
         System.out.println();
      }
   }
   static boolean knightTour(int x, int y, int move, int[] xMove, int[] yMove) {
      int xNext, yNext;
      //when the total board is covered
      if (move == N*N)     
         return true;
      for (int k = 0; k < 8; k++) {
         xNext = x + xMove[k];
         yNext = y + yMove[k];
         //check room is preoccupied or not
         if (isValid(xNext, yNext)) {     
            sol[xNext][yNext] = move;
               if (knightTour(xNext, yNext, move+1, xMove, yMove))
                  return true;
               else
                  // backtracking
                  sol[xNext][yNext] = -1;
         }
      }
      return false;
   }
   static boolean findKnightTourSol() {
      //initially set all values to -1 of solution matrix    
      for (int[] row : sol)
         Arrays.fill(row, -1);
         //all possible moves for knight
         int[] xMove = {2, 1, -1, -2, -2, -1, 1, 2};
         int[] yMove = {1, 2, 2, 1, -1, -2, -2, -1};
         //starting from room (0, 0)
         sol[0][0] = 0;     
         if (!knightTour(0, 0, 1, xMove, yMove)) {
            System.out.println("Solution does not exist");
            return false;
         } else
            displaySolution();
      return true;
   }
   public static void main(String[] args) {
      findKnightTourSol();
   }
}

N = 8

# The solution matrix
sol = [[-1 for _ in range(N)] for _ in range(N)]

# Check if place is in range and not assigned yet
def isValid(x, y):
    return (x >= 0 and x < N and y >= 0 and y < N and sol[x][y] == -1)

# Function to print the solution
def displaySolution():
    print("The possible solution: ")
    for x in range(N):
        for y in range(N):
            print(f"{sol[x][y]:3}", end=" ")
        print()

# Recursive function to solve the problem
def knightTour(x, y, move, xMove, yMove):
    if move == N*N:
        return True
    for k in range(8):
        xNext = x + xMove[k]
        yNext = y + yMove[k]
        if isValid(xNext, yNext):
            sol[xNext][yNext] = move
            if knightTour(xNext, yNext, move+1, xMove, yMove):
                return True
            else:
                # Backtracking
                sol[xNext][yNext] = -1
    return False

def findKnightTourSol():
    # All possible moves for knight
    xMove = [2, 1, -1, -2, -2, -1, 1, 2]
    yMove = [1, 2, 2, 1, -1, -2, -2, -1]
    # Starting from room (0, 0)
    sol[0][0] = 0
    if not knightTour(0, 0, 1, xMove, yMove):
        print("Solution does not exist")
        return False
    else:
        displaySolution()
    return True

if __name__ == "__main__":
    findKnightTourSol()

输出

The possible solution: 
  0  59  38  33  30  17   8  63 
 37  34  31  60   9  62  29  16 
 58   1  36  39  32  27  18   7 
 35  48  41  26  61  10  15  28 
 42  57   2  49  40  23   6  19 
 47  50  45  54  25  20  11  14 
 56  43  52   3  22  13  24   5 
 51  46  55  44  53   4  21  12
打印页面
上一页
下一页
广告