通过交换获得最大数字

什么是通过交换获得最大数字的问题？

在**通过交换获得最大数字**问题中，给定一个包含数字的字符串和一个正数'k'，我们的任务是找到通过交换给定字符串'k'次数字到不同位置而获得最大值的排列。例如，如果给定字符串N = 1739且k = 1，则可以构建的最大数字是9731。

回溯法

让我们看看解决通过交换获得最大数字问题的回溯法。假设给定的字符串是：

Input: 129814999

通过交换这些数字可以获得的最大值是：

Output: 999984211

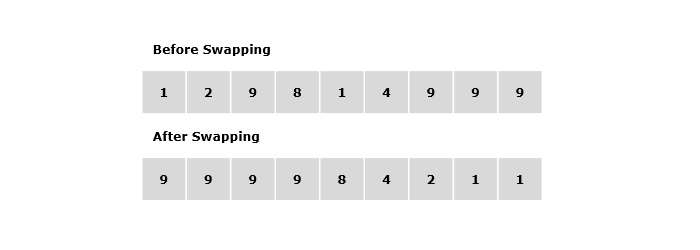
回溯法的思路是尝试给定字符串'N'中所有可能的两位数字交换，并跟踪到目前为止获得的最大数字。除了最大数字外，我们还需要跟踪我们已经执行了多少次交换，并在达到'k'时停止。

为了实现回溯法，我们需要一个主函数和一个辅助函数，它们将执行以下操作：

如果当前交换次数等于最大交换次数，则将当前数字与当前最大数字进行比较，如果需要，则更新最大数字。然后返回。
遍历当前数字中所有数字对。对于每一对，交换它们并递归调用辅助函数。
递归调用之后，交换回它们以恢复原始数字。

伪代码

以下是使用回溯法解决通过交换获得最大数字问题的伪代码：

Begin
   if swaps = 0, then
      return
   n := number of digits in the number
   for i := 0 to n-2, do
      for j := i+1 to n-1, do
         if number[i] < number[j], then
            exchange number[i] and number[j]
            if number is greater than maxNumber, then
               maxNumber := number
            maxNum(number, swaps-1, maxNumber)
            exchange number[i] and number[j] again for backtrack
      done
   done
End

示例

以下示例演示了如何在各种编程语言中使用回溯法解决通过交换获得最大数字的问题。

C语言 C++ Java Python

#include <stdio.h>
#include <string.h>
void swap(char *x, char *y) {
    char temp;
    temp = *x;
    *x = *y;
    *y = temp;
}
void mxmNumbr(char str[], int swaps, char max[]) {
   //when no swaps are left
   if(swaps == 0)        
      return;
   int n = strlen(str);
    //for every digits of given number
   for (int i = 0; i < n - 1; i++) {       
      for (int j = i + 1; j < n; j++) {
         //when ith number smaller than jth number
         if (str[i] < str[j]) {             
            swap(&str[i], &str[j]);
            //when current number is greater, make it maximum
            if (strcmp(str, max) > 0)      
               strcpy(max, str);
            //go for next swaps
            mxmNumbr(str, swaps - 1, max);   
            //when it fails, reverse the swapping
            swap(&str[i], &str[j]);        
         }
      }
   }
}
int main() {
   char str[] = "129814999";
   int swpNumbr = 4;
   char max[10];
   strcpy(max, str);
   mxmNumbr(str, swpNumbr, max);
   printf("The given number is: %s\n", str);
   printf("The maximum number is: %s\n", max);
   return 0;
}

#include <iostream>
using namespace std;
void mxmNumbr(string str, int swaps, string &max) {
   //when no swaps are left
   if(swaps == 0)        
      return;
   int n = str.length();
    //for every digits og given number
   for (int i = 0; i < n - 1; i++) {       
      for (int j = i + 1; j < n; j++) {
         //when ith number smaller than jth number
         if (str[i] < str[j]) {             
            swap(str[i], str[j]);
            //when current number is greater, make it maximum
            if (str.compare(max) > 0)      
               max = str;
            //go for next swaps
            mxmNumbr(str, swaps - 1, max);   
            //when it fails, reverse the swapping
            swap(str[i], str[j]);        
         }
      }
   }
}
int main() {
   string str = "129814999";
   int swpNumbr = 4;
   string max = str;
   mxmNumbr(str, swpNumbr, max);
   cout <<"The given number is: " <<str << endl;
   cout <<"The maximum number is: "<< max << endl;
}

import java.util.*;
public class Main {
   // Function to find maximum number after k swaps
   static void mxmNumbr(StringBuilder str, int swaps, StringBuilder max) {
      // when no swaps are left
      if (swaps == 0)
         return;
      int n = str.length();
      // for every digits of given number
      for (int i = 0; i < n - 1; i++) {
         for (int j = i + 1; j < n; j++) {
            // when ith number smaller than jth number
            if (str.charAt(i) < str.charAt(j)) {
               // swap str[i] with str[j]
                  char temp = str.charAt(i);
                  str.setCharAt(i, str.charAt(j));
                  str.setCharAt(j, temp);
                  // when current number is greater, make it maximum
                  if (str.toString().compareTo(max.toString()) > 0)
                     max.replace(0, max.length(), str.toString());
                  // go for next swaps
                  mxmNumbr(str, swaps - 1, max);
                  // when it fails, reverse the swapping
                  temp = str.charAt(i);
                  str.setCharAt(i, str.charAt(j));
                  str.setCharAt(j, temp);
             }
         }
      }
   }
   public static void main(String[] args) {
      StringBuilder str = new StringBuilder("129814999");
      int swpNumbr = 4;
      StringBuilder max = new StringBuilder(str);
      mxmNumbr(str, swpNumbr, max);
      System.out.println("The given number is: " + str);
      System.out.println("The maximum number is: " + max);
   }
}

def mxmNumbr(str, swaps, max):
    # when no swaps are left
    if swaps == 0:
        return
    n = len(str)
    # for every digits of given number
    for i in range(n - 1):
        for j in range(i + 1, n):
            # when ith number smaller than jth number
            if str[i] < str[j]:
                # swap str[i] with str[j]
                str[i], str[j] = str[j], str[i]
                # when current number is greater, make it maximum
                if str > max[0]:
                    max[0] = str[:]
                # go for next swaps
                mxmNumbr(str, swaps - 1, max)
                # when it fails, reverse the swapping
                str[i], str[j] = str[j], str[i]

def main():
    str = list("129814999")
    swpNumbr = 4
    max = [str[:]]
    mxmNumbr(str, swpNumbr, max)
    print("The given number is: ", ''.join(str))
    print("The maximum number is: ", ''.join(max[0]))

if __name__ == "__main__":
    main()

输出

The given number is: 129814999
The maximum number is: 999984211

打印页面