迷宫中的老鼠问题

上一页
下一页

迷宫中的老鼠问题是一个寻路谜题，我们的目标是从起点找到一条到达出口的最佳路径。在这个谜题中，有一只老鼠被困在一个由方形矩阵表示的迷宫中。迷宫包含不同的单元格，老鼠可以通过这些单元格到达迷宫的出口。

使用回溯法解决迷宫中的老鼠问题

假设迷宫的大小为NxN，其中单元格可以标记为1或0。标记为1的单元格表示有效路径，而标记为0的单元格表示墙壁或障碍物。请记住，老鼠可以向上、下、左、右移动，但每个单元格只能访问一次。源位置和目标位置分别是左上角和右下角单元格。

Rat in a Maze Problem

目标是找到老鼠从起始单元格（0，0）到达目标单元格（N-1，N-1）的所有可能的路径。该算法将显示一个矩阵，从中我们可以找到老鼠到达目标点的路径。下图说明了路径 -

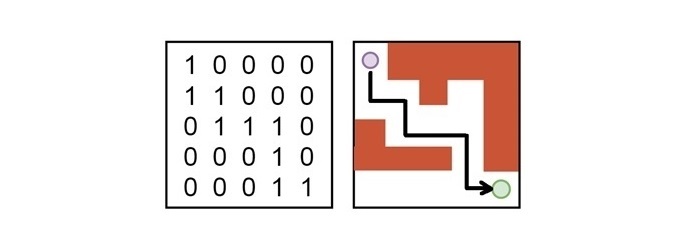
Rat in a Maze output

回溯过程通过标记已访问的单元格并从死胡同回溯来系统地探索所有可能的路径。这种方法保证了如果给定问题存在解决方案，则会找到所有可能的解决方案。

要使用回溯法解决迷宫中的老鼠问题，请遵循以下步骤 -

  • 首先，将起始单元格标记为已访问。

  • 接下来，探索所有方向以检查是否存在有效单元格。

  • 如果存在有效的未访问单元格，则移动到该单元格并将其标记为已访问。

  • 如果没有找到有效的单元格，则回溯并检查其他单元格，直到到达出口点。

示例

以下示例说明了如何在各种编程语言中解决迷宫中的老鼠问题。

C C++ Java Python
#include <stdio.h>
#define N 5
// Original maze
int maze[N][N] = {
   {1, 0, 0, 0, 0},
   {1, 1, 0, 1, 0},
   {0, 1, 1, 1, 0},
   {0, 0, 0, 1, 0},
   {1, 1, 1, 1, 1}
};
// To store the final solution of the maze path
int sol[N][N];
void showPath() {
   printf("The solution maze:\n");
   for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++)
         printf("%d ", sol[i][j]);
      printf("\n");
   }
}
// Function to check if a place is inside the maze and has value 1
int isValidPlace(int x, int y) {
   if (x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1)
      return 1;
   return 0;
}
int solveRatMaze(int x, int y) {
   // When (x,y) is the bottom right room
   if (x == N - 1 && y == N - 1) {
      sol[x][y] = 1;
      return 1;
   }
   // Check whether (x,y) is valid or not
   if (isValidPlace(x, y)) {
      // Set 1 when it is a valid place
      sol[x][y] = 1;
      // Find path by moving in the right direction
      if (solveRatMaze(x + 1, y))
         return 1;
      // When the x direction is blocked, go for the bottom direction
      if (solveRatMaze(x, y + 1))
         return 1;
      // If both directions are closed, there is no path
      sol[x][y] = 0;
      return 0;
   }
   return 0;
}
int findSolution() {
   if (solveRatMaze(0, 0) == 0) {
      printf("There is no path\n");
      return 0;
   }
   showPath();
   return 1;
}
int main() {
   findSolution();
   return 0;
}

#include<iostream>
#define N 5
using namespace std;
// original maze
int maze[N][N]  =  {
   {1, 0, 0, 0, 0},
   {1, 1, 0, 1, 0},
   {0, 1, 1, 1, 0},
   {0, 0, 0, 1, 0},
   {1, 1, 1, 1, 1}
};
 // to store the final solution of the maze path 
int sol[N][N];        
void showPath() {
   cout << "The solution maze: " << endl;   
   for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++)
         cout << sol[i][j] << " ";
      cout << endl;
   }
}
// function to check place is inside the maze and have value 1
bool isValidPlace(int x, int y) {     
   if(x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1)
      return true;
   return false;
}
bool solveRatMaze(int x, int y) {
   // when (x,y) is the bottom right room
   if(x == N-1 && y == N-1) {       
      sol[x][y] = 1;
      return true;
   }
   //check whether (x,y) is valid or not
   if(isValidPlace(x, y) == true) {     
      //set 1, when it is valid place
      sol[x][y] = 1; 
       //find path by moving right direction
      if (solveRatMaze(x+1, y) == true)      
         return true;
      //when x direction is blocked, go for bottom direction     
      if (solveRatMaze(x, y+1) == true)         
         return true;
      //if both are closed, there is no path     
      sol[x][y] = 0;         
      return false;
   }  
   return false;
}
bool findSolution() {
   if(solveRatMaze(0, 0) == false) {
      cout << "There is no path";
      return false;
   }
   showPath();
   return true;
}
int main() {
   findSolution();
}

import java.util.Arrays;
public class MazeSolverClass {
   private static final int N = 5;
   // Original maze
   private static int[][] maze = {
      {1, 0, 0, 0, 0},
      {1, 1, 0, 1, 0},
      {0, 1, 1, 1, 0},
      {0, 0, 0, 1, 0},
      {1, 1, 1, 1, 1}
   };
   // To store the final solution of the maze path
   private static int[][] sol = new int[N][N];
   // to display path
   private static void showPath() {
      System.out.println("The solution maze:");
      for (int i = 0; i < N; i++) {
         System.out.println(Arrays.toString(sol[i]));
      }
   }
   // Function to check if a place is inside the maze and has value 1
   private static boolean isValidPlace(int x, int y) {
      return x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1;
   }
   private static boolean solveRatMaze(int x, int y) {
      // When (x,y) is the bottom right room
      if (x == N - 1 && y == N - 1) {
         sol[x][y] = 1;
         return true;
      }
      // Check whether (x,y) is valid or not
      if (isValidPlace(x, y)) {
         // Set 1 when it is a valid place
         sol[x][y] = 1;
         // Find path by moving in the right direction
         if (solveRatMaze(x + 1, y)) {
            return true;
         }
         // When the x direction is blocked, go for the bottom direction
         if (solveRatMaze(x, y + 1)) {
            return true;
         }
         // If both directions are closed, there is no path
         sol[x][y] = 0;
         return false;
      }
      return false;
   }
   private static boolean findSolution() {
      return solveRatMaze(0, 0);
   }
   // main method
   public static void main(String[] args) {
      if (findSolution()) {
         showPath();
      } else {
         System.out.println("There is no path");
      }
   }
}

N = 5
# Original maze
maze = [
    [1, 0, 0, 0, 0],
    [1, 1, 0, 1, 0],
    [0, 1, 1, 1, 0],
    [0, 0, 0, 1, 0],
    [1, 1, 1, 1, 1]
]
# To store the final solution of the maze path
sol = [[0] * N for _ in range(N)]
def showPath():
    print("The solution maze:")
    for row in sol:
        print(*row)

def isValidPlace(x, y):
    return 0 <= x < N and 0 <= y < N and maze[x][y] == 1

def solveRatMaze(x, y):
    # When (x,y) is the bottom right room
    if x == N - 1 and y == N - 1:
        sol[x][y] = 1
        return True

    # Check whether (x,y) is valid or not
    if isValidPlace(x, y):
        # Set 1 when it is a valid place
        sol[x][y] = 1

        # Find path by moving in the right direction
        if solveRatMaze(x + 1, y):
            return True

        # When the x direction is blocked, go for the bottom direction
        if solveRatMaze(x, y + 1):
            return True

        # If both directions are closed, there is no path
        sol[x][y] = 0
        return False

    return False
def findSolution():
    if not solveRatMaze(0, 0):
        print("There is no path")
        return False
    showPath()
    return True

if __name__ == "__main__":
    findSolution()

输出

The solution maze:
1 0 0 0 0 
1 1 0 0 0 
0 1 1 1 0 
0 0 0 1 0 
0 0 0 1 1
打印页面
上一页
下一页
广告