数独求解算法

什么是数独？

数独是一种逻辑益智游戏，需要将一个部分填充的9x9网格用数字1到9填充，确保每一行和每一列都包含从1到9的每个数字，并且每个3x3的子网格（也称为宫）都包含从1到9的每个数字。有几种算法可以有效地解决这个难题。在本教程中，我们将学习如何使用回溯法来解决数独难题。

使用回溯法解决数独

假设给定的9x9矩阵代表一个数独网格。其中，空白单元格用0表示。最终输出矩阵（数独网格）将被填充数字。如果不存在解，则返回false。下图说明了给定数独的问题和解：

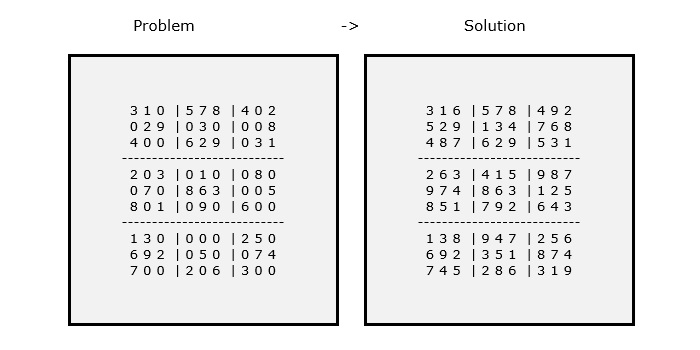
在解决数独问题的简单方法中，算法会生成从1到9的所有可能的数字组合来填充空单元格。在逐个为每个单元格赋值后，检查赋值是否有效。这种解决数独问题的方法非常冗长且耗时。

步骤

按照以下步骤使用回溯法解决数独问题：

首先，识别空单元格，用0表示。
如果找到空单元格，则检查在该单元格中放置数字是否有效，方法是检查该数字是否已存在于同一行、列或3x3子网格中。
如果可以在单元格中放置数字，则将数字分配给单元格。否则，回溯并再次分配0。

示例

在此示例中，我们将演示如何在各种编程语言中解决数独问题。

C C++ Java Python

#include <stdio.h>
#define N 9
int grid[N][N] = { 
    { 3, 1, 0, 5, 7, 8, 4, 0, 2 },
    { 0, 2, 9, 0, 3, 0, 0, 0, 8 },
    { 4, 0, 0, 6, 2, 9, 0, 3, 1 },
    { 2, 0, 3, 0, 1, 0, 0, 8, 0 },
    { 0, 7, 0, 8, 6, 3, 0, 0, 5 },
    { 8, 0, 1, 0, 9, 0, 6, 0, 0 },
    { 1, 3, 0, 0, 0, 0, 2, 5, 0 },
    { 6, 9, 2, 0, 5, 0, 0, 7, 4 },
    { 7, 0, 0, 2, 0, 6, 3, 0, 0 }
};
//check whether num is present in col or not
int isPresentInCol(int col, int num) {    
   for (int row = 0; row < N; row++)
      if (grid[row][col] == num)
         return 1;
   return 0;
}
//check whether num is present in row or not
int isPresentInRow(int row, int num) {    
   for (int col = 0; col < N; col++)
      if (grid[row][col] == num)
         return 1;
   return 0;
}
//check whether num is present in 3x3 box or not
int isPresentInBox(int boxStartRow, int boxStartCol, int num) {    
   for (int row = 0; row < 3; row++)
      for (int col = 0; col < 3; col++)
         if (grid[row+boxStartRow][col+boxStartCol] == num)
            return 1;
   return 0;
}
//print the sudoku grid after solving
void sudokuGrid() {   
   for (int row = 0; row < N; row++) {
      for (int col = 0; col < N; col++) {
         if(col == 3 || col == 6)
            printf(" | ");
         printf("%d ", grid[row][col]);
      }
      if(row == 2 || row == 5) {
         printf("\n");
         for(int i = 0; i<N; i++)
            printf("---");
      }
      printf("\n");
   }
}
//get empty location and update row and column
int findEmptyPlace(int *row, int *col) {    
   for (*row = 0; *row < N; (*row)++)
      for (*col = 0; *col < N; (*col)++)
         //marked with 0 is empty
         if (grid[*row][*col] == 0) 
            return 1;
   return 0;
}
int isValidPlace(int row, int col, int num) {
   //when item not found in col, row and current 3x3 box
   return !isPresentInRow(row, num) && !isPresentInCol(col, num) && !isPresentInBox(row - row%3 , col - col%3, num);
}
int solveSudoku() {
   int row, col;
   //when all places are filled
   if (!findEmptyPlace(&row, &col))
      return 1;     
    //valid numbers are 1 - 9      
   for (int num = 1; num <= 9; num++) { 
      //check validation, if yes, put the number in the grid 
      if (isValidPlace(row, col, num)) {    
         grid[row][col] = num;
         //recursively go for other rooms in the grid
         if (solveSudoku())     
            return 1;
         //turn to unassigned space when conditions are not satisfied    
         grid[row][col] = 0;    
      }
   }
   return 0;
}
int main() {
   if (solveSudoku() == 1)
      sudokuGrid();
   else
      printf("Can't get a solution");
}

#include <iostream>
#define N 9
using namespace std;
int grid[N][N] = { 
    { 3, 1, 0, 5, 7, 8, 4, 0, 2 },
    { 0, 2, 9, 0, 3, 0, 0, 0, 8 },
    { 4, 0, 0, 6, 2, 9, 0, 3, 1 },
    { 2, 0, 3, 0, 1, 0, 0, 8, 0 },
    { 0, 7, 0, 8, 6, 3, 0, 0, 5 },
    { 8, 0, 1, 0, 9, 0, 6, 0, 0 },
    { 1, 3, 0, 0, 0, 0, 2, 5, 0 },
    { 6, 9, 2, 0, 5, 0, 0, 7, 4 },
    { 7, 0, 0, 2, 0, 6, 3, 0, 0 }
};
//check whether num is present in col or not
bool isPresentInCol(int col, int num) {    
   for (int row = 0; row < N; row++)
      if (grid[row][col] == num)
         return true;
   return false;
}
//check whether num is present in row or not
bool isPresentInRow(int row, int num) {    
   for (int col = 0; col < N; col++)
      if (grid[row][col] == num)
         return true;
   return false;
}
//check whether num is present in 3x3 box or not
bool isPresentInBox(int boxStartRow, int boxStartCol, int num) {    
   for (int row = 0; row < 3; row++)
      for (int col = 0; col < 3; col++)
         if (grid[row+boxStartRow][col+boxStartCol] == num)
            return true;
   return false;
}
 //print the sudoku grid after solving
void sudokuGrid() {   
   for (int row = 0; row < N; row++) {
      for (int col = 0; col < N; col++) {
         if(col == 3 || col == 6)
            cout << " | ";
         cout << grid[row][col] <<" ";
      }
      if(row == 2 || row == 5) {
         cout << endl;
         for(int i = 0; i<N; i++)
            cout << "---";
      }
      cout << endl;
   }
}
//get empty location and update row and column
bool findEmptyPlace(int &row, int &col) {    
   for (row = 0; row < N; row++)
      for (col = 0; col < N; col++)
         //marked with 0 is empty
         if (grid[row][col] == 0) 
            return true;
   return false;
}
bool isValidPlace(int row, int col, int num) {
   //when item not found in col, row and current 3x3 box
   return !isPresentInRow(row, num) && !isPresentInCol(col, num) && !isPresentInBox(row - row%3 , col - col%3, num);
}
bool solveSudoku() {
   int row, col;
   //when all places are filled
   if (!findEmptyPlace(row, col))
      return true;     
    //valid numbers are 1 - 9      
   for (int num = 1; num <= 9; num++) { 
      //check validation, if yes, put the number in the grid 
      if (isValidPlace(row, col, num)) {    
         grid[row][col] = num;
         //recursively go for other rooms in the grid
         if (solveSudoku())     
            return true;
         //turn to unassigned space when conditions are not satisfied    
         grid[row][col] = 0;    
      }
   }
   return false;
}
int main() {
   if (solveSudoku() == true)
      sudokuGrid();
   else
      cout << "Can't get a solution";
}

public class Main {
    static int N = 9;
    static int[][] grid = { 
        { 3, 1, 0, 5, 7, 8, 4, 0, 2 },
        { 0, 2, 9, 0, 3, 0, 0, 0, 8 },
        { 4, 0, 0, 6, 2, 9, 0, 3, 1 },
        { 2, 0, 3, 0, 1, 0, 0, 8, 0 },
        { 0, 7, 0, 8, 6, 3, 0, 0, 5 },
        { 8, 0, 1, 0, 9, 0, 6, 0, 0 },
        { 1, 3, 0, 0, 0, 0, 2, 5, 0 },
        { 6, 9, 2, 0, 5, 0, 0, 7, 4 },
        { 7, 0, 0, 2, 0, 6, 3, 0, 0 }
    };
    //check whether num is present in col or not
    static boolean isPresentInCol(int col, int num) {    
       for (int row = 0; row < N; row++)
          if (grid[row][col] == num)
             return true;
       return false;
    }
    //check whether num is present in row or not
    static boolean isPresentInRow(int row, int num) {    
       for (int col = 0; col < N; col++)
          if (grid[row][col] == num)
             return true;
       return false;
    }
    //check whether num is present in 3x3 box or not
    static boolean isPresentInBox(int boxStartRow, int boxStartCol, int num) {    
       for (int row = 0; row < 3; row++)
          for (int col = 0; col < 3; col++)
             if (grid[row+boxStartRow][col+boxStartCol] == num)
                return true;
       return false;
    }
    //print the sudoku grid after solving
    static void sudokuGrid() {   
       for (int row = 0; row < N; row++) {
          for (int col = 0; col < N; col++) {
             if(col == 3 || col == 6)
                System.out.print(" | ");
             System.out.print(grid[row][col] + " ");
          }
          if(row == 2 || row == 5) {
             System.out.println();
             for(int i = 0; i<N; i++)
                System.out.print("---");
          }
          System.out.println();
       }
    }
    //get empty location and update row and column
    static int[] findEmptyPlace() {    
       for (int row = 0; row < N; row++)
          for (int col = 0; col < N; col++)
             //marked with 0 is empty
             if (grid[row][col] == 0) 
                return new int[] {row, col};
       return null;
    }
    static boolean isValidPlace(int row, int col, int num) {
       //when item not found in col, row and current 3x3 box
       return !isPresentInRow(row, num) && !isPresentInCol(col, num) && !isPresentInBox(row - row%3 , col - col%3, num);
    }
    static boolean solveSudoku() {
       int row, col;
       int[] emptyPlace = findEmptyPlace();
       if (emptyPlace == null)
          return true;     
        //valid numbers are 1 - 9      
       for (int num = 1; num <= 9; num++) { 
          //check validation, if yes, put the number in the grid 
          if (isValidPlace(emptyPlace[0], emptyPlace[1], num)) {    
             grid[emptyPlace[0]][emptyPlace[1]] = num;
             //recursively go for other rooms in the grid
             if (solveSudoku())     
                return true;
             //turn to unassigned space when conditions are not satisfied    
             grid[emptyPlace[0]][emptyPlace[1]] = 0;    
          }
       }
       return false;
    }
    public static void main(String[] args) {
       if (solveSudoku() == true)
          sudokuGrid();
       else
          System.out.println("Can't get a solution");
    }
}

# Define the size of the grid
N = 9

# Initialize the grid
grid = [
    [3, 1, 0, 5, 7, 8, 4, 0, 2],
    [0, 2, 9, 0, 3, 0, 0, 0, 8],
    [4, 0, 0, 6, 2, 9, 0, 3, 1],
    [2, 0, 3, 0, 1, 0, 0, 8, 0],
    [0, 7, 0, 8, 6, 3, 0, 0, 5],
    [8, 0, 1, 0, 9, 0, 6, 0, 0],
    [1, 3, 0, 0, 0, 0, 2, 5, 0],
    [6, 9, 2, 0, 5, 0, 0, 7, 4],
    [7, 0, 0, 2, 0, 6, 3, 0, 0]
]
# Check whether num is present in col or not
def isPresentInCol(col, num):
    for row in range(N):
        if grid[row][col] == num:
            return True
    return False

# Check whether num is present in row or not
def isPresentInRow(row, num):
    for col in range(N):
        if grid[row][col] == num:
            return True
    return False

# Check whether num is present in 3x3 box or not
def isPresentInBox(boxStartRow, boxStartCol, num):
    for row in range(3):
        for col in range(3):
            if grid[row+boxStartRow][col+boxStartCol] == num:
                return True
    return False

# Print the sudoku grid after solving
def sudokuGrid():
    for row in range(N):
        for col in range(N):
            if col == 3 or col == 6:
                print(" | ", end="")
            print(grid[row][col], end=" ")
        if row == 2 or row == 5:
            print("\n" + "---"*N)
        print()

# Get empty location and update row and column
def findEmptyPlace():
    for row in range(N):
        for col in range(N):
            # Marked with 0 is empty
            if grid[row][col] == 0:
                return row, col
    return None, None

def isValidPlace(row, col, num):
    # When item not found in col, row and current 3x3 box
    return not isPresentInRow(row, num) and not isPresentInCol(col, num) and not isPresentInBox(row - row%3, col - col%3, num)

def solveSudoku():
    row, col = findEmptyPlace()

    # When all places are filled
    if row is None and col is None:
        return True

    # Valid numbers are 1 - 9
    for num in range(1, 10):
        # Check validation, if yes, put the number in the grid
        if isValidPlace(row, col, num):
            grid[row][col] = num

            # Recursively go for other rooms in the grid
            if solveSudoku():
                return True

            # Turn to unassigned space when conditions are not satisfied
            grid[row][col] = 0

    return False

if __name__ == "__main__":
    if solveSudoku():
        sudokuGrid()
    else:
        print("Can't get a solution")

输出

3 1 6  | 5 7 8  | 4 9 2 
5 2 9  | 1 3 4  | 7 6 8 
4 8 7  | 6 2 9  | 5 3 1 
---------------------------
2 6 3  | 4 1 5  | 9 8 7 
9 7 4  | 8 6 3  | 1 2 5 
8 5 1  | 7 9 2  | 6 4 3 
---------------------------
1 3 8  | 9 4 7  | 2 5 6 
6 9 2  | 3 5 1  | 8 7 4 
7 4 5  | 2 8 6  | 3 1 9

打印页面