
- 数据结构与算法
- DSA - 首页
- DSA - 概述
- DSA - 环境搭建
- DSA - 算法基础
- DSA - 渐进分析
- 数据结构
- DSA - 数据结构基础
- DSA - 数据结构和类型
- DSA - 数组数据结构
- 链表
- DSA - 链表数据结构
- DSA - 双向链表数据结构
- DSA - 循环链表数据结构
- 栈与队列
- DSA - 栈数据结构
- DSA - 表达式解析
- DSA - 队列数据结构
- 搜索算法
- DSA - 搜索算法
- DSA - 线性搜索算法
- DSA - 二分搜索算法
- DSA - 插值搜索
- DSA - 跳跃搜索算法
- DSA - 指数搜索
- DSA - 斐波那契搜索
- DSA - 子列表搜索
- DSA - 哈希表
- 排序算法
- DSA - 排序算法
- DSA - 冒泡排序算法
- DSA - 插入排序算法
- DSA - 选择排序算法
- DSA - 归并排序算法
- DSA - 希尔排序算法
- DSA - 堆排序
- DSA - 桶排序算法
- DSA - 计数排序算法
- DSA - 基数排序算法
- DSA - 快速排序算法
- 图数据结构
- DSA - 图数据结构
- DSA - 深度优先遍历
- DSA - 广度优先遍历
- DSA - 生成树
- 树数据结构
- DSA - 树数据结构
- DSA - 树的遍历
- DSA - 二叉搜索树
- DSA - AVL树
- DSA - 红黑树
- DSA - B树
- DSA - B+树
- DSA - 伸展树
- DSA - 字典树
- DSA - 堆数据结构
- 递归
- DSA - 递归算法
- DSA - 使用递归实现汉诺塔
- DSA - 使用递归实现斐波那契数列
- 分治法
- DSA - 分治法
- DSA - 最大最小值问题
- DSA - Strassen矩阵乘法
- DSA - Karatsuba算法
- 贪心算法
- DSA - 贪心算法
- DSA - 旅行商问题(贪心算法)
- DSA - Prim最小生成树
- DSA - Kruskal最小生成树
- DSA - Dijkstra最短路径算法
- DSA - 地图着色算法
- DSA - 分数背包问题
- DSA - 带截止日期的作业调度
- DSA - 最优合并模式算法
- 动态规划
- DSA - 动态规划
- DSA - 矩阵链乘法
- DSA - Floyd Warshall算法
- DSA - 0-1背包问题
- DSA - 最长公共子序列算法
- DSA - 旅行商问题(动态规划)
- 近似算法
- DSA - 近似算法
- DSA - 顶点覆盖算法
- DSA - 集合覆盖问题
- DSA - 旅行商问题(近似算法)
- 随机化算法
- DSA - 随机化算法
- DSA - 随机化快速排序算法
- DSA - Karger最小割算法
- DSA - Fisher-Yates洗牌算法
- DSA 有用资源
- DSA - 问答
- DSA - 快速指南
- DSA - 有用资源
- DSA - 讨论
后缀数组算法
后缀数组是一种数据结构,用于存储给定字符串的所有后缀的字典序。它对于各种字符串处理问题非常有用,例如模式匹配、搜索、查找最长公共前缀等等。这个数组可以快速找到模式在一个较大的文本中的位置。
后缀数组如何工作?
假设文本为“Carpet”。要构建其后缀数组,请按照以下步骤操作:
生成给定文本的所有后缀。在这种情况下,可能的后缀可能是“carpet”、“arpet”、“rpet”、“pet”、“et”、“t”。
对所有后缀进行排序。所有按排序顺序排列的后缀为“arpet”、“carpet”、“et”、“pet”、“rpet”和“t”。
因此,后缀数组如下:[1, 0, 4, 3, 2, 5]。
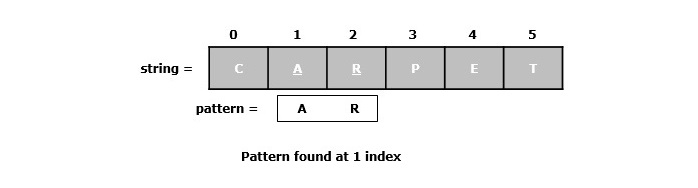
要将此后缀数组用于模式匹配,我们可以在排序后的后缀上执行二分搜索,以查找以模式开头的后缀的范围。例如,让我们取上述字符串“Carpet”,我们想找到模式“ar”,我们可以将其与后缀数组中的中间后缀“pet”进行比较。
由于“ar”小于此后缀,因此我们可以丢弃后缀数组的右半部分,并在左半部分继续二分搜索。最终,我们会发现以“ar”开头的后缀在原始字符串中的位置为“1”。
让我们看看后缀数组的输入输出场景:
Input: string: "AABABCEDBABCDEB" Output: Pattern found at index: 3 Pattern found at index: 9 Pattern found at index: 1
示例
以下示例说明了后缀数组在模式匹配中的工作原理。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// Structure of suffixes
struct Suffix {
int index;
char suff[100];
};
// Function to compare two suffixes for sorting
int strCompare(const void* a, const void* b) {
struct Suffix* s1 = (struct Suffix*)a;
struct Suffix* s2 = (struct Suffix*)b;
return strcmp(s1->suff, s2->suff);
}
// Function to fill the suffix array
int* fillSuffixArray(char* txt, int n) {
struct Suffix* suffixes = (struct Suffix*) malloc(n * sizeof(struct Suffix));
// Store suffixes and their indexes in an array
for (int i = 0; i < n; i++) {
suffixes[i].index = i;
strncpy(suffixes[i].suff, &(txt[i]), n - i);
suffixes[i].suff[n-i] = '\0';
}
// Sort the suffixes
qsort(suffixes, n, sizeof(struct Suffix), strCompare);
// Store indexes of all sorted suffixes in the suffix array
int* suffixArr = (int*) malloc(n * sizeof(int));
for (int i = 0; i < n; i++)
suffixArr[i] = suffixes[i].index;
// Deallocate the dynamic memory
free(suffixes);
return suffixArr;
}
// binary search on suffix array and find all occurrences of pattern
void suffixArraySearch(char* pat, char* txt, int* suffixArr, int n) {
int m = strlen(pat);
// binary search for pattern in text using the built suffix array
int l = 0, r = n - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
char substr[100];
strncpy(substr, &(txt[suffixArr[mid]]), m);
substr[m] = '\0';
int res = strncmp(pat, substr, m);
if (res == 0) {
printf("Pattern found at index: %d\n", suffixArr[mid]);
// Move to the left of mid
int temp = mid - 1;
while (temp >= 0 && strncmp(pat, &(txt[suffixArr[temp]]), m) == 0) {
printf("Pattern found at index: %d\n", suffixArr[temp]);
temp--;
}
// Move to the right of mid
temp = mid + 1;
while (temp < n && strncmp(pat, &(txt[suffixArr[temp]]), m) == 0) {
printf("Pattern found at index: %d\n", suffixArr[temp]);
temp++;
}
return;
}
if (res < 0) r = mid - 1;
else l = mid + 1;
}
printf("Pattern not found\n");
}
int main() {
char txt[] = "AAAABCAEAAABCBDDAAAABC";
// pattern to be searched
char pat[] = "AAABC";
int n = strlen(txt);
int* suffixArr = fillSuffixArray(txt, n);
suffixArraySearch(pat, txt, suffixArr, n);
free(suffixArr);
return 0;
}
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
// Structure of suffixes
struct Suffix {
int index;
string suff;
};
// Function to compare two suffixes for sorting
bool strCompare(Suffix a, Suffix b) {
return a.suff < b.suff;
}
// Function to fill the suffix array
int* fillSuffixArray(string txt, int n) {
Suffix* suffixes = new Suffix[n];
// Storing suffixes and indexes in an array
for (int i = 0; i < n; i++) {
suffixes[i].index = i;
suffixes[i].suff = txt.substr(i, n - i);
}
// Sorting the suffixes
sort(suffixes, suffixes+n, strCompare);
// Store indexes of all sorted suffixes in suffix array
int* suffixArr = new int[n];
for (int i = 0; i < n; i++)
suffixArr[i] = suffixes[i].index;
// Deallocate the dynamic memory
delete[] suffixes;
return suffixArr;
}
// binary search on the suffix array and find all occurrences of pattern
void suffixArraySearch(string pat, string txt, int* suffixArr, int n) {
int m = pat.length();
// binary search for the pattern
int l = 0, r = n - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
string substr = txt.substr(suffixArr[mid], m);
if (pat == substr) {
cout << "Pattern found at index: " << suffixArr[mid] << endl;
// Move to the left of mid
int temp = mid - 1;
while (temp >= 0 && txt.substr(suffixArr[temp], m) == pat) {
cout << "Pattern found at index: " << suffixArr[temp] << endl;
temp--;
}
// Move to the right of mid
temp = mid + 1;
while (temp < n && txt.substr(suffixArr[temp], m) == pat) {
cout << "Pattern found at index: " << suffixArr[temp] << endl;
temp++;
}
return;
}
if (pat < substr) r = mid - 1;
else l = mid + 1;
}
cout << "Pattern not found" << endl;
}
int main() {
string txt = "AAAABCAEAAABCBDDAAAABC";
// pattern to be searched
string pat = "AAABC";
int n = txt.length();
int* suffixArr = fillSuffixArray(txt, n);
suffixArraySearch(pat, txt, suffixArr, n);
delete[] suffixArr;
return 0;
}
import java.util.Arrays;
public class Main {
// Structure of suffixes
static class SuffixCmpr implements Comparable<SuffixCmpr> {
int index;
String suff;
// Constructor
public SuffixCmpr(int index, String suff) {
this.index = index;
this.suff = suff;
}
// to sort suffixes alphabetically
public int compareTo(SuffixCmpr other) {
return this.suff.compareTo(other.suff);
}
}
// method to build a suffix array
public static int[] fillsuffixArray(String s) {
int n = s.length();
SuffixCmpr[] suffixes = new SuffixCmpr[n];
// Create and sort suffixes
for (int i = 0; i < n; i++) {
suffixes[i] = new SuffixCmpr(i, s.substring(i));
}
Arrays.sort(suffixes);
// Store indexes of all sorted suffixes
int[] fillsuffixArray = new int[n];
for (int i = 0; i < n; i++) {
fillsuffixArray[i] = suffixes[i].index;
}
return fillsuffixArray;
}
// method to search a pattern in a text using suffix array
public static void suffixArraySearch(String pattern, String txt, int[] suffArr) {
int n = txt.length();
int m = pattern.length();
// binary search for the pattern in the text using suffix array
int l = 0, r = n - 1;
while (l <= r) {
int mid = l + (r - l) / 2;
int res = pattern.compareTo(txt.substring(suffArr[mid], Math.min(suffArr[mid] + m, n)));
if (res == 0) {
System.out.println("Pattern found at index: " + suffArr[mid]);
// Move to previous suffix in the sorted array
int temp = mid - 1;
while (temp >= 0 && txt.substring(suffArr[temp], Math.min(suffArr[temp] + m, n)).equals(pattern)) {
System.out.println("Pattern found at index: " + suffArr[temp]);
temp--;
}
// Move to next suffix in the sorted array
temp = mid + 1;
while (temp < n && txt.substring(suffArr[temp], Math.min(suffArr[temp] + m, n)).equals(pattern)) {
System.out.println("Pattern found at index: " + suffArr[temp]);
temp++;
}
return;
}
if (res < 0) r = mid - 1;
else l = mid + 1;
}
System.out.println("Pattern not found");
}
public static void main(String[] args) {
String txt = "AAAABCAEAAABCBDDAAAABC";
String pattern = "AAABC";
// Filling the suffix array
int[] suffArr = fillsuffixArray(txt);
// Calling method to Search pattern in suffix array
suffixArraySearch(pattern, txt, suffArr);
}
}
def fill_suffix_array(txt):
# Array of tuples, each tuple stores the index and suffix
suffixes = [(i, txt[i:]) for i in range(len(txt))]
# Sort the suffixes
suffixes.sort(key=lambda x: x[1])
# Return the list of indices after sorting
return [suff[0] for suff in suffixes]
def suffixArraySearch(pat, txt, suffix_arr):
n = len(txt)
m = len(pat)
# Iterate over the suffix array
for i in range(n):
if txt[suffix_arr[i]:min(suffix_arr[i] + m, n)] == pat:
print(f"Pattern found at index: {suffix_arr[i]}")
def main():
txt = "AAAABCAEAAABCBDDAAAABC"
pat = "AAABC"
suffix_arr = fill_suffix_array(txt)
suffixArraySearch(pat, txt, suffix_arr)
if __name__ == "__main__":
main()
输出
Pattern found at index: 8 Pattern found at index: 1 Pattern found at index: 17
后缀数组的复杂度
使用后缀数组进行模式匹配的优点是它只需要 O(m log n) 时间,其中 m 是模式的长度,n 是字符串的长度。缺点是首先构建后缀数组需要 O(n log n) 时间和 O(n) 空间。
广告