DSA - 模式搜索

上一页
下一页

什么是模式搜索？

模式搜索/匹配算法是一种用于在给定文本中定位或查找特定模式或子字符串的技术。其基本思想是在指定的数据结构中查找特定模式的所有出现情况。例如，给定一个数字数组[1, 2, 3, 4, 5, 6, 3, 4, 9]，我们需要在数组中查找模式[3, 4]的所有出现情况。答案将是索引号2和6。

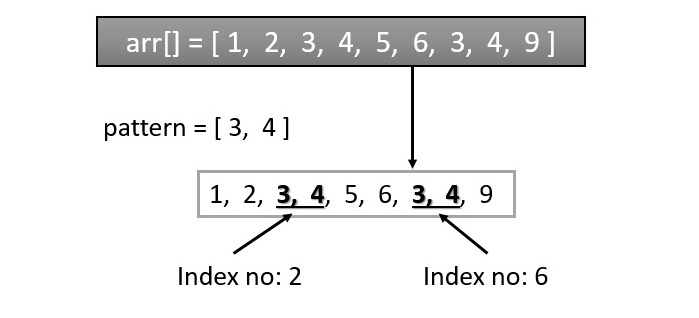
Pattern Matching

模式搜索算法如何工作？

有多种模式搜索算法以不同的方式工作。设计这些类型算法的主要目标是降低时间复杂度。对于较长的文本，传统方法可能需要大量时间才能完成模式搜索任务。

如果我们说传统方法，我们实际上是指蛮力法来解决模式搜索问题。让我们看看它是如何工作的 -

  • 将模式滑过文本。

  • 逐个比较每个字符。

  • 如果所有字符都匹配，则表示找到匹配项。

  • 如果不是，则将模式向右移动一个位置，并重复此过程，直到到达文本末尾或找到匹配项。

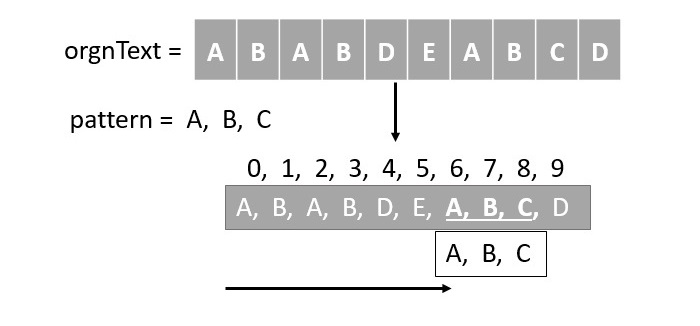
Pattern Solving

请记住，蛮力法是解决字符串匹配或搜索的最简单方法，但它也是最慢、效率最低的方法。该算法的时间复杂度为O(nm)，其中'n'是文本的长度，'m'是模式的长度。这意味着在最坏情况下，我们必须将文本的每个字符与模式的每个字符进行比较，如果n和m很大，这可能会非常慢。下一节中还提到了其他算法。

示例

在本例中，我们将实际演示蛮力法在各种编程语言中解决模式匹配问题。

C C++ Java Python
#include <stdio.h>
#include <string.h>
// method to find match
void findMatch(char *orgText, char *pattern) {
   int n = strlen(orgText);
   int m = strlen(pattern);
   // comparing the text and pattern one by one
   for (int i = 0; i <= n-m; i++) {
      int j = 0;
      while (j < m && orgText[i+j] == pattern[j]) {
         j++;
      }
      // print result if found
      if (j == m) {
         printf("Oohhoo! Match found at index: %d\n", i);
         return; 
      }
   }
   // if not found
   printf("Oopps! No match found\n");
}
int main() {
   // Original Text
   char orgText[] = "Tutorials Point";
   // pattern to be matched
   char pattern[] = "Point";
   // method calling
   findMatch(orgText, pattern); 
   return 0;
}

#include <iostream>
#include <string>
using namespace std;
// method to find match
void findMatch(string orgText, string pattern) {
   int n = orgText.length();
   int m = pattern.length();
   // comparing the text and pattern one by one
   for (int i = 0; i <= n-m; i++) {
      int j = 0;
      while (j < m && orgText[i+j] == pattern[j]) {
         j++;
      }
      // print result if found
      if (j == m) {
         cout << "Oohhoo! Match found at index: " << i << endl;
         return; 
      }
   }
   // if not found
   cout << "Oopps! No match found" << endl;
}
int main() {
   // Original Text
   string orgText = "Tutorials Point";
   // pattern to be matched
   string pattern = "Point";
   // method calling
   findMatch(orgText, pattern); 
   return 0;
}

public class PattrnMatch {
   public static void main(String[] args) {
      // Original Text
      String orgText = "Tutorials Point";
      // pattern to be matched
      String pattern = "Point";
      // method calling
      findMatch(orgText, pattern); 
   }
   // method to find match
   public static void findMatch(String orgText, String pattern) {
      int n = orgText.length();
      int m = pattern.length();
      // comparing the text and pattern one by one
      for (int i = 0; i <= n-m; i++) {
         int j = 0;
         while (j < m && orgText.charAt(i+j) == pattern.charAt(j)) {
            j++;
         }
         // print result if found
         if (j == m) {
            System.out.println("Oohhoo! Match found at index: " + i);
               return; 
            }
      }
	  // if not found
	  System.out.println("Oopps! No match found");
   }
}

# method to find match
def findMatch(orgText, pattern):
   n = len(orgText)
   m = len(pattern)
   # comparing the text and pattern one by one
   for i in range(n-m+1):
      j = 0
      while j < m and orgText[i+j] == pattern[j]:
         j += 1
      # print result if found
      if j == m:
         print("Oohhoo! Match found at index:", i)
         return 
   # if not found
   print("Oopps! No match found")
# Original Text
orgText = "Tutorials Point"
# pattern to be matched
pattern = "Point"
# method calling
findMatch(orgText, pattern)

输出

Oohhoo! Match found at index: 10

数据结构中的模式搜索算法

可以在数据结构上应用各种模式搜索技术来检索某些模式。只有当模式搜索操作返回所需元素或其索引时，才认为该操作成功，否则，该操作被视为不成功。

以下是我们将在本教程中介绍的模式搜索算法列表 -

模式搜索算法的应用

模式搜索算法的应用如下 -

  • 生物信息学 - 它是一个将模式搜索算法应用于分析生物数据（例如DNA和蛋白质结构）的领域。
  • 文本处理 - 文本处理涉及从文档集中查找字符串的任务。对于剽窃检测、拼写和语法检查、搜索引擎查询等至关重要。
  • 数据安全 - 模式匹配算法可用于数据安全，通过建立恶意软件检测和密码识别系统。
  • 情感分析 - 通过匹配或检测单词的语气，我们可以分析用户的口音、情绪和情感。
  • 推荐系统 - 我们还可以通过模式匹配算法分析视频、音频或任何博客的内容，这将进一步有助于推荐其他内容。
打印页面
上一页
下一页
广告