能力倾向 - 解析几何

---

---

平面上的点的位置

在坐标几何中，点放置在“坐标平面”上，如下所示。它有两个刻度 - 一个横跨平面称为“x 轴”，另一个与之成直角称为 y 轴。（这些可以被认为类似于上面段落中的列和行。）轴线交叉的点称为原点，x 和 y 都为零。

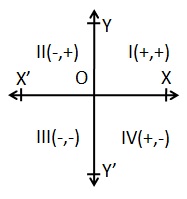
在 x 轴上，右边的值为正，左边的值为负。在 y 轴上，原点上方的值为正，原点下方的值为负。平面上的点的位置由两个数字给出；第一个表示它在 x 轴上的位置，第二个表示它在 y 轴上的位置。它们一起定义了平面上唯一的单一位置。因此，在上图中，点 A 的 x 值为 20，y 值为 15。这些是点 A 的坐标，有时称为其“直角坐标”。

请注意，顺序很重要；x 坐标始终是这对中的第一个。

两点之间的距离

如果 A(x₁,y₁) 和 B (x₂,y₂) 是两点，则

AB =√(x2-x1)2 + (y2-y1)2

点到原点的距离

点 A(x, y) 到原点 O(0, 0) 的距离由下式给出

OA =√(x2+y2)

三角形的面积

如果 A(x₁,y₁)、B(x₂,y₂) 和 C= (X₃, Y₃) 是 ∆ABC 的三个顶点，则其面积由下式给出

∆ = 1/2 {x1(y2- Y3)+ x2(Y3- Y1) +X3(y1-y2)}

三点共线的条件

三点 A(x₁,y₁)、B(x₂,y₂) 和 C= (X₃, Y₃) 共线当且仅当 ar(√ABC)= 0。

∴ A、B、C 共线 ⇒ x₁(y₂- Y₃)+ x₂(Y₃- Y₁) +X₃(y₁-y₂) = 0

点分割线段

如果点 p(x,y) 以 m:n 的比例分割 A(x₁,y₁) 和 B(x₂,y₂) 的连线，则

X= (mx2+nx1)/m+n and Y =(my2+ny1)/m+n

如果 A(x₁,y₁) 和 B(x₂,y₂) 是线段 AB 的端点，则 AB 中点的坐标为

[(x1 + x2)/ 2 , (y1 + y2)/ 2]

三角形的重心

三角形所有中线的交点称为其重心。如果 A(x₁,y₁)、B(x₂,y₂) 和 C= (X₃, Y₃) 是 ABC 的顶点，则其重心的坐标为 { (1/3 (x₁+x₂+x₃),1/3 (y₁+y₂+Y₃)}

各种类型的四边形

四边形是

• 如果其对边相等且对角线相等，则为矩形。

• 如果其对边相等且对角线不相等，则为平行四边形但不是矩形。

• 如果所有边都相等且对角线相等，则为正方形。

• 如果所有边都相等且对角线不相等，则为菱形但不是正方形。

直线的方程

• x 轴的方程为 y =0。

• y 轴的方程为 x = 0。

• 与 y 轴平行且与之相距 a 的直线的方程为 x= a。

• 与 x 轴平行且与之相距 b 的直线的方程为 y= b。

• 经过点 A(x₁,y₁) 和 B(x₂,y₂) 的直线的方程为 y-y₁/ x-x₁ = y₂-y₁/x₂-x₁。此直线的斜率为 y₂-y₁/x₂-x₁。

• 直线在斜截式中的方程为 Y= mx+ c，其中 m 是其斜率。

解题示例

解题示例