高低和距离 - 例题解析

题1 - 从距离塔底375米的一点，观察塔顶的仰角为45°，则塔高（米）为？

答案 - A

解释

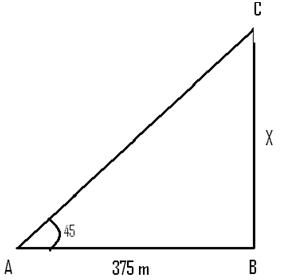
From the right angled triangle
Tan(45°)=  X/375
=> X = 375 m

题2 - 在距离塔底90米的一点，塔顶的仰角为cot^-1(4/5)。则塔高为

答案 - C

解释

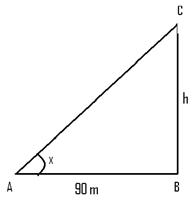
Let cot^-1(4/5) = x 
=> cotx =  4/5   
=> tan(x) = 5/4   
From the right angled triangle
Tan(x) =  h/90 
=> h = 5/4*90 =112.5 m

题3 - 在平地上，塔顶的仰角为30°。靠近20米后，仰角变为45°。则塔高为

答案 - C

解释

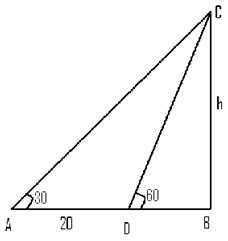
Let h be the height of tower
From figure.
20 =h (  cot30 - cot60)	
20 =h (√3-1/√3) 
=> 20√3 = h (3-1) 
=> h=10√3.

题4 - 从连接两座垂直塔的塔底中点观察两座塔顶的仰角分别为45°和60°。两塔高度的比例是

答案 - B

解释

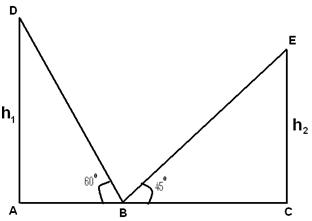
Tan(60)=h₁/AB
=> h1=√3AB
Tan(45)=h₁/BC
=> h2=BC
h1/ h2=√3/1
=> h1:h2=√3:1

题5 - 两座塔的高度分别为90米和45米。连接其塔顶的直线与水平面成45°角，则两塔之间的距离是

答案 - B

解释

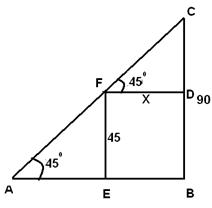
Let the distance between the towers be X 
From the right angled triangle CFD 
Tan(45)=  (90-45)/X   
=> x=45 meters

题6 - 从平地上的P点，观察塔顶的仰角为60°。如果塔高180米，则P点到塔底的距离是

答案 - A

解释

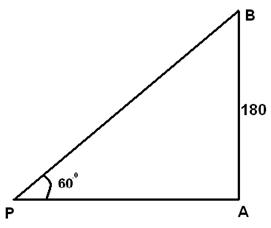
From ∠APB = 60° and AB = 180 m.
AB/AP= tan 60° =√3
AP=AB/√3 =180/√3=60√3

题7 - 一座25米高的塔顶与电线杆底部之间的仰角为45°，与电线杆顶部之间的仰角为30°。求电线杆的高度。

答案 - B

解释

Let AB be the tower and CD be the electric pole. 
From the figure CA = DE
=> 25/(Tan(45))=(25-h)/(Tan(30))
=> 25  Tan(30) = 25-h
=> h=25-25Tan(30)
=25(1- Tan(30)) 
=25((√3-1)/√3)

题8 - 一个1.4米高的人距离塔10√3米。从他的眼睛到塔顶的仰角为60°。塔高为

答案 - D

解释

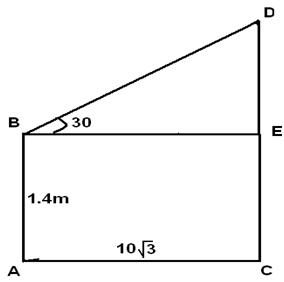
Let AB be the observer and CD be the tower.
Then, CE = AB = 1.4 m,
 BE = AC = 10v3 m.
DE/BE=Tan (30) =1/√3
DE=10√3/√3=10
CD=CE+DE=1.4+10=11.4 m

题9 - 一人在塔顶观察一艘快速远离塔的船。当船距离塔75米时，船与人的视线的俯角为60°。10秒后，俯角变为45°。假设船在静水中航行，则船的近似速度是多少？

答案 - D

解释

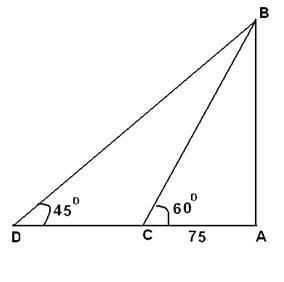
Let AB be the tower and C and D be the positions of the boat.
Distance travelled by boat = CD
From the figure 75tan(60)=(75+CD)tan(45)
=>75√3 = 75+CD
=>CD =55 m
Speed = distance/time=55/10
=5.5 m/sec=19.8 kmph

题10 - 两座塔之间的水平距离为90米。从180米高的第二座塔顶观察第一座塔顶的俯角为45°。则第一座塔高为

答案 - C

解释

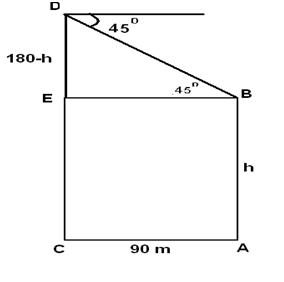
=>(180-h)/90 = Tan(45)
=> h =90 m

aptitude_height_distance.htm

打印页面