- 能力倾向有用资源
- 能力倾向 - 问答
几何 - 在线测验
以下测验提供与几何相关的多项选择题 (MCQ)。您需要阅读所有给出的答案,然后点击正确的答案。如果您不确定答案,可以使用显示答案按钮查看答案。您可以使用下一题按钮查看测验中的新一组问题。

答案:D
解释
The sum of all angle around a point is 360⁰ .
答案:A
解释
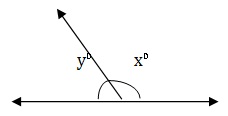
x+y = 180 ⇒ x+ 4/5 x = 180 ⇒ 5x +4x = 900 ⇒ 9x=900 ⇒ x = 100.
答案:B
解释
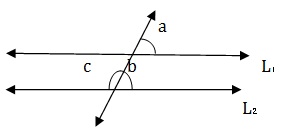
∠B = ∠A = 65⁰ (corr. ∠s). ∴ ∠B +∠C= 180⁰ ⇒ 65⁰ +∠C = 180⁰ ⇒ ∠C = ( 180⁰ - 65⁰) = 115⁰.
答案:A
解释
(∠A+∠B) +(∠B+∠C) =(65⁰+140⁰)= 205⁰ ⇒ (∠A+∠B+∠C) +∠B =205⁰ ⇒ 180⁰ +∠B=205⁰ ⇒ ∠B =(205-180)⁰ =25⁰
答案:B
解释
∠ A- ∠B = 33⁰ and ∠B -∠C =18⁰ ⇒ A= 33+ B and C=B -18 = (33+B) + B + (B-18) =180 ⇒ 3B =165 ⇒ B 55. ∴ ∠B =55⁰.
答案:C
解释
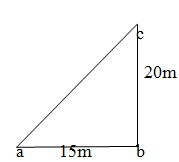
Let BC be the wall and AB be the ladder. Then , BC = 20 m and AC =15m ∴ AB2= BC2 +AC2 = (20)2 + (15)2 = (400 + 225) = 625 ⇒ AB = √625 = 25m.
答案:D
解释
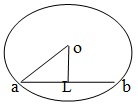
Let O be the center of the circle and AB be the chord . Form O, draw OL ⊥ AB. join OA. Then, oA = 13 cm and OL = 12cm. ∴ AL2 = OA2 -OL2=(13)2 - (12)2= (169-144) =25. =.> AL= √25 =5 cm ⇒ AB = 2 * AL =(2*5) cm = 10 cm.
答案:A
解释
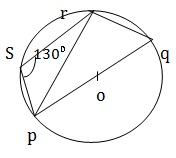
PQRS is a cyclic quadrilateral. ∠PSR + ∠PQR = 180⁰ ⇒ 130⁰ + ∠PQR =180⁰⇒∠ PQR=50⁰. Also PRQ = 90⁰ (angle in a semi- circle) In PQR we have ∠PQR + ∠PRQ + ∠RPQ = 180⁰⇒ 50⁰ +90⁰+∠RPQ =180⁰ ⇒ ∠RPQ = 40⁰.
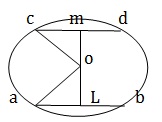
第 9 题 - AB 和 CD 是圆心两侧的两条平行弦。如果 AB = 10 厘米,CD= 24 厘米,圆的半径为 13 厘米,则两弦之间的距离是
答案:A
解释
From O draw OL⊥ AB and OM CD. Join OA and OC. AL = 1/2 AB = 5cm , OA = 13 cm. OL2 = OA2 - AL2 = (13) 2 - 52 = (169 - 25) = 144 ⇒ OL = √144 = 12 cm. Now ,CM =1/2 * CD =12 cm and OC =13cm. ∴ OM2 = OC2 - CM2 = (13) 2 - (12) 2 = (169 - 144) = 25 ⇒ OM =√ 25 = 5cm. ∴ ML = OM + OL = (5+12 ) cm =17cm.
答案:B
解释
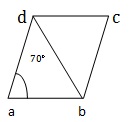
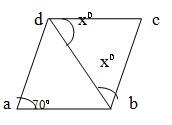
Let CDB= x⁰. then , CD = CB ⇒ ∠CBD = ∠CDB = x⁰. ∠ BCD = ∠BAD = 70⁰ (opp. s of a rhombus) ∴ x+x + 70 = 180 (sum of the ∠ s of a ∆ is 180⁰) ⇒ 2x = 110 ⇒ x=55. ∴ ∠CDB= 55⁰.
aptitude_geometry.htm
广告