几何 - 例题解析

答案 - D

解释

A line has no points.

答案 - B

解释

A line segment has two end points.

答案 - A

解释

A ray has one end point.

答案 - B

解释

An angle which is greater than 180°  but less than 360° is called a reflex angle.

答案 - B

解释

Complement of 62°= (90° – 62°) = 28°.

答案 - B

解释

Supplement of 60° = (180°-60°) =120°.

答案 - C

解释

Complement of 72° 40' = (90°-72° 40') =17° 20'.

答案 - B

解释

x = 1/5 (180 – x )⇒ 5x = 180 – x ⇒ 6x = 180 ⇒ x = 30°.

答案 - B

解释

x=(90-x) ⇒ 2x = 90 ⇒ x = 45° .

答案 - D

解释

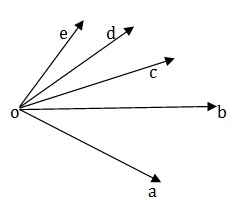
The angle are ∠AOB , ∠BOC,∠COD,∠DOE,∠AOC,∠AOD, ∠AOE,∠BOD,∠BOD,∠COE. 
Thus , 10 angle are  formed.

答案 - A

解释

x – (90-x ) = 24 ⇒ 2x = 114 ⇒ x = 57
∴ Required angle is 57°.

答案 - A

解释

(180 –X) – X = 32 ⇒  2x = 180 – 32 = 148 ⇒ x = 74. 
Required angle is 74°.

答案 - C

解释

Let the measures of the angle be (3x)° and (2x)°. Then, 
3x+2x=180 ⇒ 5x = 180 ⇒ x = 36.
Smaller angle = (2x)° = (2*36)° = 72°. 

答案 - A

解释

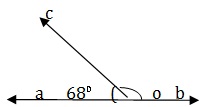
Since ∠AOB is a straight angle , we have
X+ 68 = 180 ⇒ x= (180-68)°  = 120°

答案 - B

解释

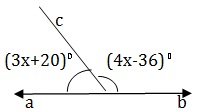
Since ∠AOB is a straight angle , we have 
∠AOC + ∠ BOC  =180° 
⇒ 3x + 20 +4x – 36 = 180
⇒ 7x = 164 ⇒ x = 22.

答案 - A

解释

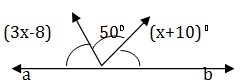
Since ∠AOB is a straight angle , we have
∠AOC  + ∠ COB  + ∠ BOD  = 180° 
⇒ (3X – 8)° + 50° + (X+ 10)° = 180° 
⇒ 4X = 128 ⇒ X = 32.