能力倾向 - 几何

---

---

点

点是一个精确的位置。

线段

两点 A 和 B 之间的直线路径称为线段 AB。线段有两个端点。

射线

将线段 AB 向一个方向无限延伸，我们就得到了射线 AB。射线 AB 只有一个端点，即 A。

直线

将线段 AB 向两个方向无限延伸，就称为直线 AB。

1. 一条直线上包含无限多个点。

2. 通过一个给定点，可以画出无限多条直线。

3. 过两个给定点 A 和 B，只能画出一条直线。

4. 两条直线相交于一点。

5. 两个平面相交于一条直线。

共线

在给定图形中，点 A、B、C 共线。

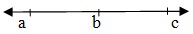
共点线

三条或多条相交于同一点的直线称为共点线。

角

两条具有共同端点 O 的射线 OA 和 OB 形成角 AOB，写成∠AOB。

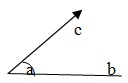
角的度量

从 OA 到 OB 的旋转量称为∠AOB 的度量，写成 m(∠AOB)。

360° 的角

如果一条射线 OA 从其初始位置 OA 开始，绕 O 逆时针方向旋转，并在完成一次旋转后回到其初始位置，那么我们就说它旋转了 360 度。这个完整的旋转被分成 360 个相等的部分。然后，每个部分称为 1 度，写成 1°。

1° = 60 分钟，写成 60'。

1 分钟 = 60 秒，写成 60"。

角的类型

1. 直角 - 度数为 90° 的角称为直角。

2. 锐角 - 度数小于 90° 的角称为锐角。

3. 钝角 - 度数大于 90° 但小于 180° 的角称为钝角。

4. 平角 - 度数为 180° 的角称为平角。

5. 优角 - 度数大于 180° 但小于 360° 的角称为优角。

6. 周角 - 度数为 360° 的角称为周角。

7. 相等角 - 如果两个角的度数相同，则称这两个角相等。

8. 余角 - 如果两个角的度数之和为 90 度，则称这两个角为余角。例如，度数为 65° 和 25° 的角是余角。

9. 补角 - 如果两个角的度数之和为 180 度，则称这两个角为补角。例如，度数为 70° 和 110° 的角是补角。

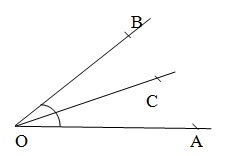
10. 邻角 - 如果两个角具有相同的顶点和一条公共边，并且非公共边位于公共边的两侧，则称这两个角为邻角。在给定图形中，∠AOC 和∠BOC 是邻角。

    

重要结果

如果一条射线落在一条直线上，那么形成的两个邻角的和为 180°。在给定图形中，射线 CP 落在直线 AB 上。

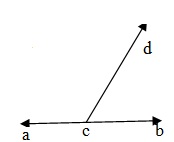
∴ ∠ACD + ∠BCD = 180°.
     

在直线上给定点的一侧形成的所有角的和为 180°。在给定图形中，在 AOB 的同一侧形成了四个角。

   
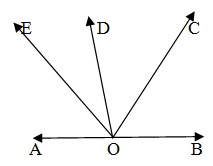
∴ ∠AOE + ∠EOD + ∠DOC + ∠COD = 180°.
  

围绕一点的所有角的和为 360°。在给定图形中，围绕点 O 形成了五个角。

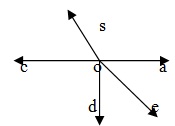
∴∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA=360°.
  

对顶角

如果两条直线 AB 和 CD 相交于点 O，则 AOC、BOD 和 BOC、AOD 是一对对顶角。对顶角总是相等的。

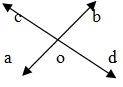
∴ ∠AOC = ∠BOD and ∠AOD = ∠BOC

平行线

如果两条直线位于同一平面内，并且无论向哪一侧延长都不相交，则称这两条直线为平行线，我们写成 L||m。

横截线截平行线

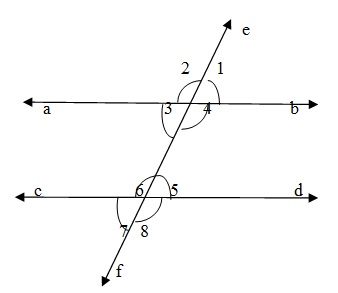
设两条平行线 AB 和 CD 被一条横截线 EF 截断。然后

同位角相等。

(∠1 = ∠5), (∠4= ∠8 ), (∠2 = ∠6) , (∠3 = ∠7)

内错角相等。

(∠3 =∠5 )  and  (∠4 =∠6 )

同旁内角互补。

∠4+∠5 = 180° and ∠3 +∠6 = 180°.                                               

三角形

由三条直线围成的图形称为三角形。在给定图形中，我们有△ABC；△ABC 有三个顶点 A、B、C。它有三个角，即∠A、∠B 和∠C。它有三条边，即 AB、AC 和 BC。

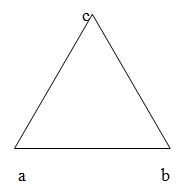
三角形的类型

1. 三条边都相等的三角形称为等边三角形。

2. 有两条边相等的三角形称为等腰三角形。

3. 三条边长度都不相同的三角形称为不等边三角形。

4. 其中一个角为 90° 的三角形称为直角三角形。

5. 其中一个角在 90° 和 180° 之间的三角形称为钝角三角形。

6. 每个角都是锐角的三角形称为锐角三角形。

7. 三角形三条边的和称为三角形的周长。

8. 三角形两条边的和大于第三条边。

9. 在直角三角形 ABC 中，∠B = 90°，我们有 AC² =AB²+BC²。这称为勾股定理。

四边形

由四条直线围成的图形称为四边形。四边形所有角的和为 360°。

1. 矩形 - 如果四边形的对边相等且每个角都是 90°，则该四边形称为矩形。在给定图中，ABCD 是一个矩形。

   

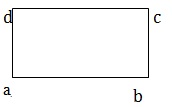
2. 正方形 - 如果四边形的所有边都相等且每个角都为 90°，则该四边形称为正方形。在给定图中，ABCD 是一个正方形，其中 AB = BC = CD = DA。

   

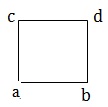
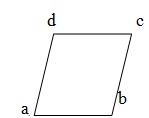
3. 平行四边形 - 如果四边形的对边平行，则该四边形称为平行四边形。在给定图中，ABCD 是一个平行四边形，其中 AB = DC & AD = BC。

   

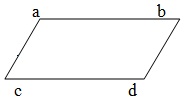
4. 菱形 - 所有边都相等的平行四边形称为菱形。在给定图中，ABCD 是一个菱形，其中 AB =BC =CD=DA，AB || DC 和 AD || BC。

   

重要事实

1. 如果四边形的对边相等且对角线相等，则该四边形为矩形。

2. 如果四边形的所有边都相等且对角线相等，则该四边形为正方形。

3. 如果四边形的对边相等，则该四边形为平行四边形。

4. 如果四边形的对边相等但对角线不相等，则该四边形为平行四边形，但不是矩形。

5. 如果四边形的所有边都相等但对角线不相等，则该四边形为菱形，但不是正方形。

关于四边形的结论

1. 在平行四边形中，我们有

   1. 对边相等。

   2. 对角相等。

   3. 每条对角线都平分平行四边形。

   4. 平行四边形的对角线互相平分。

2. 矩形的对角线相等。

3. 菱形的对角线互相垂直平分。

关于圆的结论

1. 从圆心到弦的垂线平分弦。

2. 过三个不共线的点，只有一个圆。

3. 半圆中的角是直角。

4. 圆内接四边形的对角互补。

5. 圆中同一条弧所对的圆周角相等。

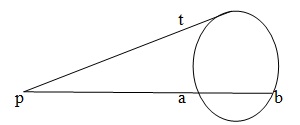
6. 圆的切线在切点处垂直于过切点的半径。

7. 从圆外一点到圆的两条切线相等。

8. 如果 PT 是圆的切线，PAB 是割线，则 PA x PB= PT²

解题示例

解题示例