Matplotlib - 色图归一化

---

---

术语归一化指的是将实数值重新缩放到一个共同的范围，例如 0 到 1 之间。它通常用作数据处理和分析中的预处理技术。

Matplotlib 中的色图归一化

在这种情况下，归一化是将数据值映射到颜色的过程。Matplotlib 库提供了各种归一化技术，包括：

• 对数

• 居中

• 对称对数

• 幂律

• 离散边界

• 双斜率

• 自定义归一化

线性归一化

Matplotlib 中的默认行为是根据指定范围内的数值线性映射颜色。此范围通常由matplotlib.colors.Normalize()实例参数的最小值 (vmin) 和最大值 (vmax) 定义。

此映射分两个步骤进行，首先将输入数据归一化到 [0, 1] 范围，然后映射到色图中的索引。

示例

此示例使用 matplotlib.colors 模块中的Normalize()类演示了 Matplotlib 的线性归一化过程。

import matplotlib as mpl
from matplotlib.colors import Normalize

# Creates a Normalize object with a specified range
norm = Normalize(vmin=-1, vmax=1)

# Normalizing a value
normalized_value = norm(0)

# Display the normalized value
print('Normalized Value', normalized_value)

输出

执行上述代码后，我们将获得以下输出：

Normalized Value: 0.5

虽然线性归一化是默认的，并且通常适用，但在某些情况下，非线性映射可能更具信息量或视觉吸引力。

对数归一化

这是一种常见的变换，它采用数据的对数（以 10 为底）。当显示跨不同尺度的变化时，这很有用。colors.LogNorm() 类用于此归一化。

示例

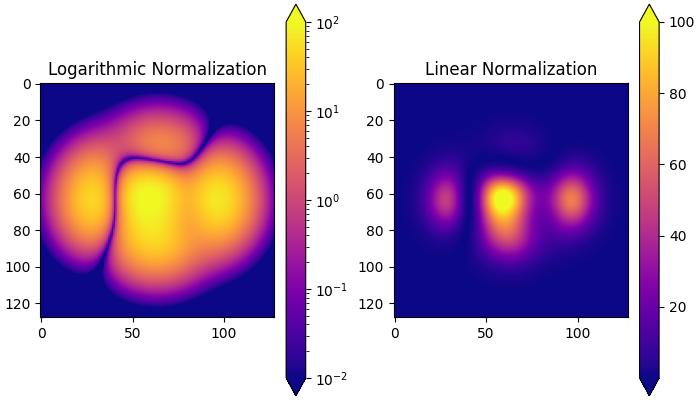
在此示例中，创建了两个子图以演示对数归一化和线性归一化变换之间的差异。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors

# Sample Data
X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)

# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7,4), layout='constrained')

# Logarithmic Normalization 
pc = ax[0].imshow(Z**2 * 100, cmap='plasma',
   norm=colors.LogNorm(vmin=0.01, vmax=100))
fig.colorbar(pc, ax=ax[0], extend='both')
ax[0].set_title('Logarithmic Normalization')

# Linear Normalization
pc = ax[1].imshow(Z**2 * 100, cmap='plasma',
   norm=colors.Normalize(vmin=0.01, vmax=100))
fig.colorbar(pc, ax=ax[1], extend='both')
ax[1].set_title('Linear Normalization')
plt.show()

输出

执行上述代码后，我们将获得以下输出：

居中归一化

当数据围绕中心对称（例如，围绕 0 的正异常和负异常）时，可以使用colors.CenteredNorm()类。它会自动将中心映射到 0.5，并将与中心偏差最大的点映射到 1.0 或 0.0，具体取决于其值。

示例

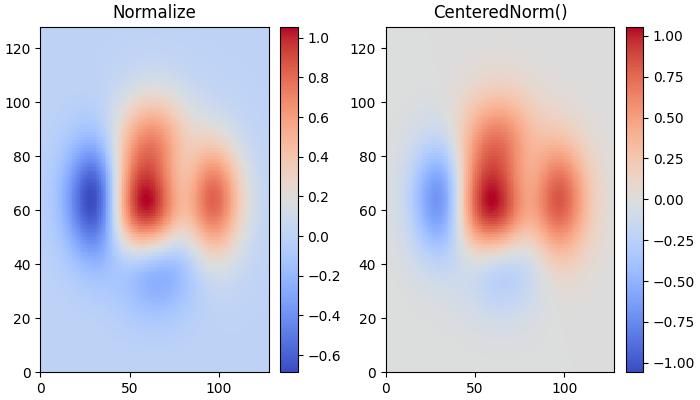
此示例比较了默认线性归一化和居中归一化 (CenteredNorm()) 对数据集的影响，使用 coolwarm 色图。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors, cm

X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)

# select a divergent colormap
cmap = cm.coolwarm 

# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7,4), layout='constrained')

# Default Linear Normalization
pc = ax[0].pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax[0])
ax[0].set_title('Normalize')

# Centered Normalization
pc = ax[1].pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax[1])
ax[1].set_title('CenteredNorm()')

plt.show()

输出

执行上述代码后，我们将获得以下输出：

对称对数归一化

如果数据可能包含正值和负值，并且希望对两者都进行对数缩放。Matplotlib 中的colors.SymLogNorm()类专为这种情况而设计。此归一化将负数对数映射到较小的值，并将正数映射到较大的值。

示例

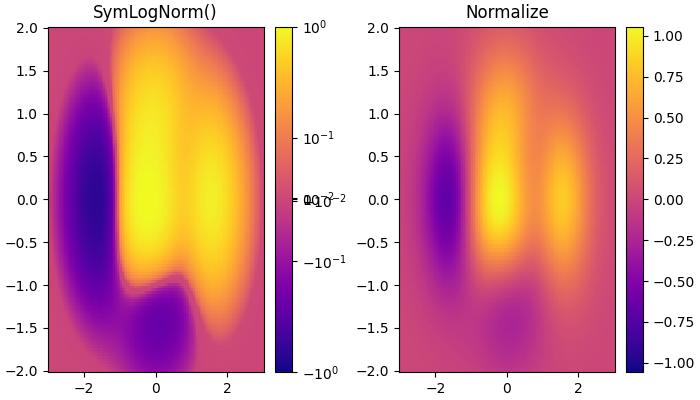
这是一个使用colors.SymLogNorm()类转换数据的示例。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors, cm

X, Y = np.mgrid[-3:3:complex(0, 128), -2:2:complex(0, 128)]
Z = (1 - X/2 + X**5 + Y**3) * np.exp(-X**2 - Y**2)

# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7, 4), layout='constrained')

# Symmetric Logarithmic Normalization
pcm = ax[0].pcolormesh(X, Y, Z, 
   norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,vmin=-1.0, vmax=1.0, base=10),
   cmap='plasma', shading='auto')
fig.colorbar(pcm, ax=ax[0])
ax[0].set_title('SymLogNorm()')

# Default Linear Normalization
pcm = ax[1].pcolormesh(X, Y, Z, cmap='plasma', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1])
ax[1].set_title('Normalize')

plt.show()

输出

执行上述代码后，我们将获得以下输出：

幂律归一化

此归一化可用于使用colors.PowerNorm()类将颜色重新映射到幂律关系。

示例

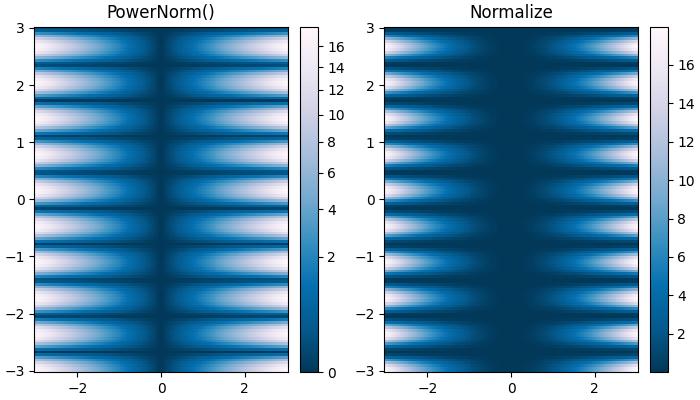
这是一个比较幂律 (colors.PowerNorm()) 和线性归一化的示例。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors, cm

X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 + np.sin(Y * 10.)) * X**2

# Create subplots
fig, ax = plt.subplots(1, 2, figsize=(7, 4), layout='constrained')

# Power-law Normalization
pcm = ax[0].pcolormesh(X, Y, Z, norm=colors.PowerNorm(gamma=0.5),
   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0])
ax[0].set_title('PowerNorm()')

# Default Linear Normalization
pcm = ax[1].pcolormesh(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1])
ax[1].set_title('Normalize')

plt.show()

输出

执行上述代码后，我们将获得以下输出：

离散边界归一化

Matplotlib 提供的另一种归一化是colors.BoundaryNorm。当需要在指定边界之间映射数据并使用线性分布的颜色时，这特别有用。

示例

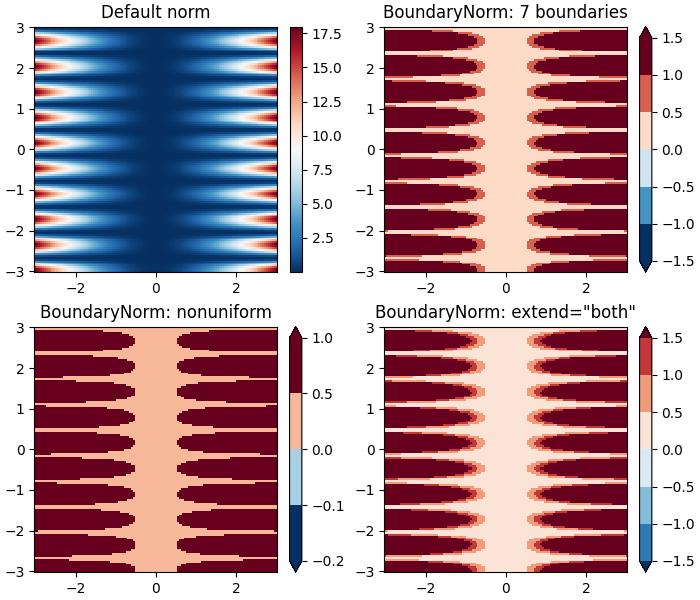
此示例演示了使用BoundaryNorm()类进行离散边界归一化的用法，以便在显示 colormesh 图时创建不同的视觉效果。

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.colors as colors

X, Y = np.meshgrid(np.linspace(-3, 3, 128), np.linspace(-3, 3, 128))
Z = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 2, figsize=(7, 6), layout='constrained')
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')

plt.show()

输出

执行上述代码后，我们将获得以下输出：

TwoSlopeNorm归一化用于在概念中心点两侧使用不同的色图，它通常用于诸如地形图之类的场景，其中陆地和海洋具有不同的海拔和深度范围。

当内置规范不足时，FuncNorm允许使用任意函数进行自定义归一化。

此外，Matplotlib 支持创建自定义归一化，例如MidpointNormalize，这对于在专业可视化中定义映射很有用。

这些工具提供了灵活性，可以将颜色表示适应不同的数据和可视化需求。