Matplotlib - 刻度

---

---

Matplotlib 中的刻度是什么？

在 Matplotlib 库中，刻度是指将数据值映射到绘图物理尺寸的过程。它们决定了数据值如何在绘图的坐标轴上表示和可视化。Matplotlib 支持各种类型的刻度，刻度的选择会显著影响数据在可视化中的呈现方式。

以下是 Matplotlib 库中常见的几种刻度类型。

• 线性刻度 − 适用于大多数数值数据，且数据幅度变化不大。
• 对数刻度 − 适用于覆盖多个数量级或呈现指数增长的数据集。
• 对称对数刻度 − 适用于同时包含正值和负值的数据集。

让我们逐一了解这些刻度。

线性刻度

线性刻度是默认用于表示绘图坐标轴上数据的刻度。它是一种简单的映射，其中数据值与其实际数值成正比地绘制。在线性刻度中，坐标轴上的相等距离表示数据值的相等差异。

线性刻度的特征

• 等间隔 − 在线性刻度中，坐标轴上的相等距离对应于数据值的相等差异。
• 线性映射 − 数据值与其在坐标轴上的位置之间的关系是线性的。

使用线性刻度

默认情况下，Matplotlib 库对 x 轴和 y 轴都使用线性刻度。要显式设置线性刻度，我们不需要使用任何特定函数，因为这是默认行为。但是，我们可以使用plt.xscale('linear')或plt.yscale('linear')分别显式指定 x 轴或 y 轴的线性刻度。

以下是将线性刻度应用于绘图的示例。

示例

import matplotlib.pyplot as plt
x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]
plt.plot(x, y)
plt.xlabel('X-axis')
plt.ylabel('Y-axis')
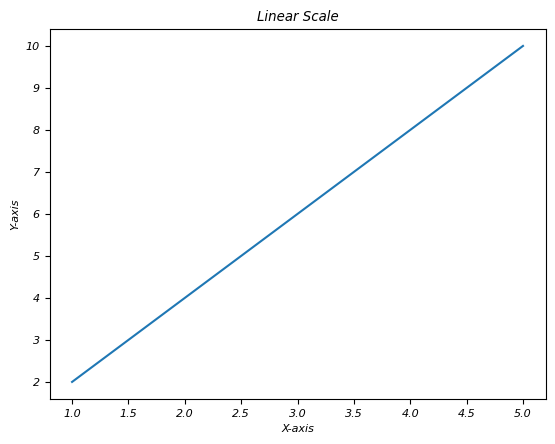
plt.title('Linear Scale')
plt.show()

输出

以下是上述程序的输出结果：

何时使用线性刻度

• 当数据没有指数增长或值的范围不太大时，通常使用线性刻度。
• 它适用于表示大多数没有表现出明显非线性行为的数值数据。

对数刻度

对数刻度使用对数映射来表示数据。当值的范围很广时，这很有用，对数刻度有助于强调较小值的变化。

对数刻度的特征

以下是对数刻度的特征：

• 等比例 − 在对数刻度中，坐标轴上的相等距离表示值之间的相等比率，而不是相等差异。
• 数据压缩 − 它将广泛的数据压缩到更易于阅读和解释的可视化中。
• 强调较小值 − 它比强调较大值更强调较小值的变化。

使用对数刻度

要使用对数刻度，我们必须分别对 x 轴或 y 轴指定 plt.xscale('log') 或 plt.yscale('log')。对数刻度在可视化指数增长或覆盖多个数量级的现象时特别有用。

何时使用对数刻度

对数刻度适用于数据幅度变化很大或需要突出显示较小值变化的情况。在金融（股票价格）、科学研究（分贝水平、地震震级）和生物学（pH 值）等领域中常用。

示例

以下是带有对数刻度的示例绘图：

import matplotlib.pyplot as plt
import numpy as np

# Generating logarithmically spaced data
x = np.linspace(1, 10, 100)
y = np.log(x)

# Creating a plot with a logarithmic scale for the x-axis
plt.plot(x, y)
plt.xscale('log')  # Set logarithmic scale for the x-axis
plt.xlabel('X-axis (log scale)')
plt.ylabel('Y-axis')
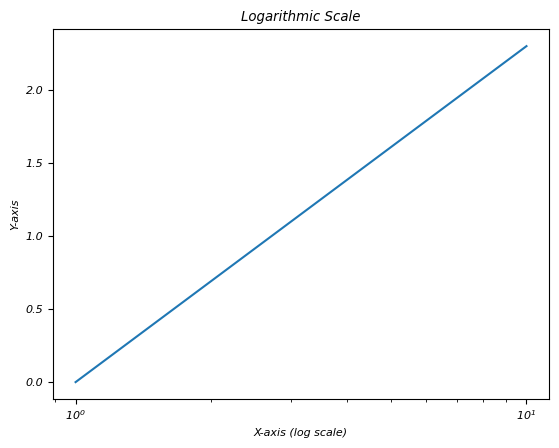
plt.title('Logarithmic Scale')
plt.show()

输出

以下是上述程序的输出结果：

在绘图中使用对数刻度可以提供对具有广泛值的数据的见解，从而更容易在同一绘图中可视化不同尺度上的模式和趋势。

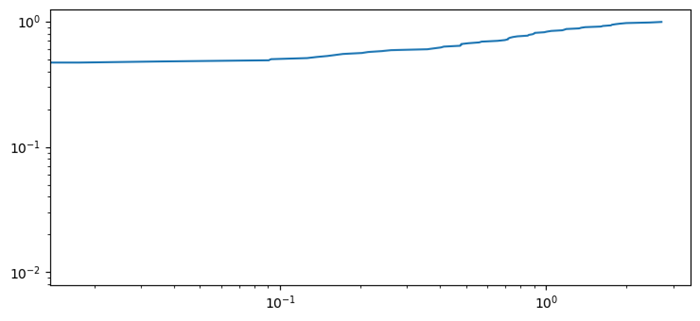
累积分布函数的对数图

下面给出的示例显示了累积分布函数的对数图。

示例

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [7.50, 3.50]
plt.rcParams["figure.autolayout"] = True
N = 100
data = np.random.randn(N)
X2 = np.sort(data)
F2 = np.array(range(N))/float(N)
plt.plot(X2, F2)
plt.xscale('log')
plt.yscale('log')
plt.show()

输出

以下是上述程序的输出结果：

对称对数刻度

对称对数刻度类似于对数刻度。它通常缩写为symlog，这是一种用于表示坐标轴上数据的刻度类型，其中值使用对数间隔对称分布在零周围。它为正值和负值都提供类似对数的刻度，同时容纳零。

要在 x 轴和 y 轴上应用对称对数刻度，我们必须分别使用plt.xscale('symlog')和plt.yscale('symlog')。

对称对数刻度的特征

对称对数刻度具有以下特征。

• 对称行为 − 以对数方式表示正值和负值，同时处理零。
• 零附近线性 − 在指定范围内（linthresh）零附近的刻度是线性的，然后过渡到对数行为。

对称对数刻度的参数

linthresh − 线性阈值，用于确定零附近刻度在过渡到对数刻度之前表现为线性的范围。

何时使用对称对数刻度

• 零附近的数据 − 适用于包含以零为中心且具有广泛正值和负值的数据集。
• 避免对称偏差 − 当需要对正值和负值进行对称表示且不偏向任何一方时。

对称对数刻度的重要性

对称对数刻度提供了一种类似对数的刻度，可以容纳正值和负值，使其适用于可视化围绕零平衡分布的数据集。

它还有助于突出显示围绕零的较小变化，同时容纳较大的值而不会歪曲表示。

示例

在此图中，我们使用plt.yscale('symlog', linthresh=0.01)在y轴上创建对称对数刻度。

import matplotlib.pyplot as plt
import numpy as np

# Generating data for a sine wave with values around zero
x = np.linspace(-10, 10, 500)
y = np.sin(x)

# Creating a plot with a symmetrical logarithmic scale for the y-axis
plt.plot(x, y)

# Set symmetrical logarithmic scale for the y-axis
plt.yscale('symlog', linthresh=0.01)  
plt.xlabel('X-axis')
plt.ylabel('Y-axis (symlog scale)')
plt.title('Symmetrical Logarithmic Scale')
plt.show()

输出

以下是上述程序的输出结果：

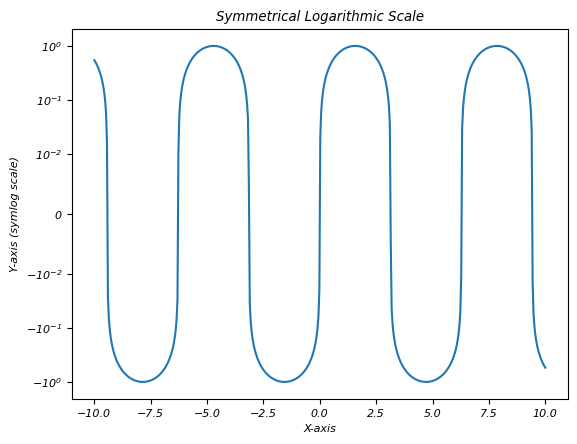
在 Matplotlib 中使用对称对数刻度可以可视化包含围绕零的值的数据集，因为它能够有效地表示和分析对称分布的数据。调整线性阈值 (linthresh) 参数对于确定刻度在零附近线性变化的范围至关重要，然后过渡到对数刻度。

Logit 刻度

Logit 刻度是一种专门类型的刻度，用于表示轴上的数据，其中值限制在 0 和 1 之间。它专门设计用于此范围内存在的数据，通常在概率或表示概率的值中遇到。

设置刻度

plt.xscale() 和 plt.yscale() 函数可分别用于设置 x 轴和 y 轴的刻度。

Logit 刻度的特征

以下是 Logit 刻度的特征。

• 约束数据 - 特别用于介于 0 和 1 之间的数据。
• 转换 - 利用 logit 函数将值从标准逻辑分布映射。

何时使用 Logit 刻度

• 概率数据 - 适用于可视化概率或表示概率的值，尤其是在处理逻辑回归或逻辑模型时。
• 0 到 1 范围内的数据 - 特别设计用于介于 0 到 1 之间的数据。

Logit 刻度的重要性

• Logit 刻度有助于可视化和分析表示概率或具有概率解释的数据。
• 它还有助于理解和可视化概率相关数据的转换。

示例 1

在此图中，我们在 x 轴和 y 轴上创建 Logit 刻度。

import matplotlib.pyplot as plt
import numpy as np

# Generating data within the 0 to 1 range
x = np.linspace(0.001, 0.999, 100)
y = np.log(x / (1 - x))

# Creating a plot with a logit scale for the x-axis
plt.plot(x, y)
plt.xscale('logit')  # Set logit scale for the x-axis
plt.xlabel('X-axis (logit scale)')
plt.ylabel('Y-axis')
plt.title('Logit Scale')
plt.show()

输出

以下是上述程序的输出结果：

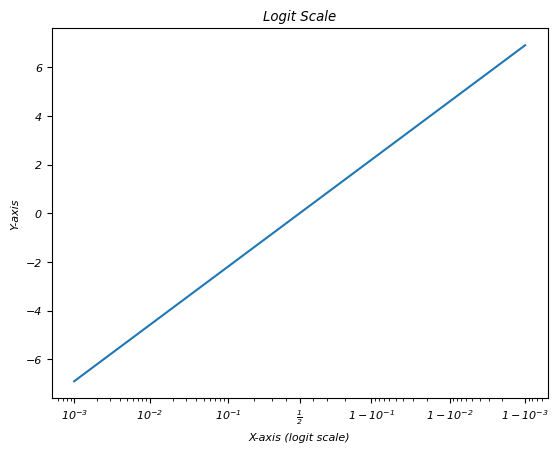
理解并选择合适的绘图刻度对于准确表示底层数据并确保模式和趋势在可视化中得到有效传达非常重要。

示例 2

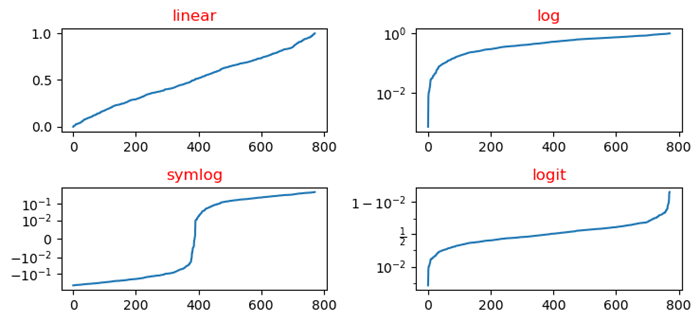
在此图中，我们按名称绘制了 yscale 类线性、对数、logit 和 symlog。

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = [7.50, 3.50]
plt.rcParams["figure.autolayout"] = True
y = np.random.normal(loc=0.5, scale=0.4, size=1000)
y = y[(y > 0) & (y < 1)]
y.sort()
x = np.arange(len(y))

# linear
plt.subplot(221)
plt.plot(x, y)
plt.yscale('linear')
plt.title('linear')

# log
plt.subplot(222)
plt.plot(x, y)
plt.yscale('log')
plt.title('log')

# symmetric log
plt.subplot(223)
plt.plot(x, y - y.mean())
plt.yscale('symlog', linthresh=0.01)
plt.title('symlog')

# logit
plt.subplot(224)
plt.plot(x, y)
plt.yscale('logit')
plt.title('logit')
plt.show()

输出

以下是上述程序的输出结果：