Matplotlib - 填充螺旋线

一般定义中，螺旋线是一种几何曲线，它从中心点发出，并随着绕中心点旋转而逐渐远离。螺旋线呈现螺旋状图案，并有多种形式，包括阿基米德螺旋线和对数螺旋线。请参见下图作为参考：

另一方面，填充螺旋线是指螺旋曲线的可视化表示，其中螺旋线包围的空间填充了颜色或图案。

在本教程中，我们将看到使用 Matplotlib 创建和填充螺旋线的两种不同方法。该过程包括定义表示螺旋线的数学方程，然后使用诸如pyplot.fill()之类的函数为螺旋线包围的区域着色。

创建基本的填充螺旋线

可以使用参数方程在极坐标中定义基本的填充螺旋线。然后使用pyplot.fill()函数用颜色填充螺旋线包围的区域。

示例

这是一个使用pyplot.fill()和np.concatenate()函数创建基本填充螺旋线的示例。

import matplotlib.pyplot as plt
import numpy as np

# Define parameters
theta = np.radians(np.linspace(0,360*5,1000))
a = 1
b = 0.2

fig, axes = plt.subplots(figsize=(7, 4))

# Create a spiral
for dt in np.arange(0, 2 * np.pi, np.pi / 2.0):
   x = a * np.cos(theta + dt) * np.exp(b * theta)
   y = a * np.sin(theta + dt) * np.exp(b * theta)

   dt = dt + np.pi / 4.0

   x2 = a * np.cos(theta + dt) * np.exp(b * theta)
   y2 = a * np.sin(theta + dt) * np.exp(b * theta)

   # Concatenate points for filling
   xf = np.concatenate((x, x2[::-1]))
   yf = np.concatenate((y, y2[::-1]))

   # Fill the spiral
   plt.fill(xf, yf)

# Display the plot
plt.show()

输出

执行上述代码后，我们将获得以下输出：

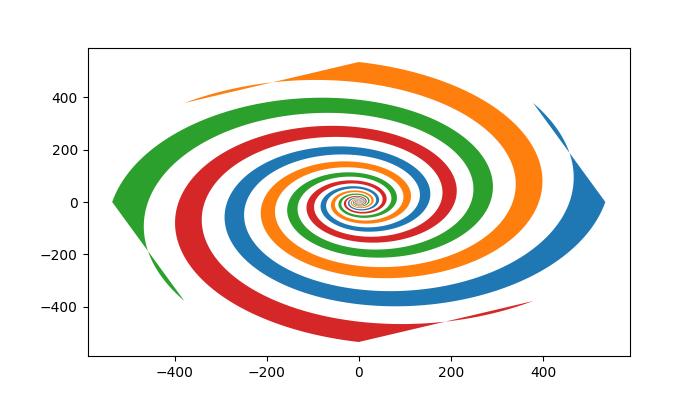
创建对数填充螺旋线

对数螺旋线是一种特殊的螺旋线，其半径随角度呈指数增长。

示例

此示例将对数螺旋线分成几部分构建，将具有不同参数的线段组合在一起。

import matplotlib.pyplot as plt
import numpy as np

# Define parameters for the logarithmic spiral
a = 2
b = 0.2

# Generate theta and radius values for different pieces
theta1 = np.linspace(0, np.pi * 3.0, 1000, endpoint=True)
r1 = np.exp(b * theta1) * a

theta2 = np.linspace(np.pi, np.pi * 4.0, 1000, endpoint=True)
r2 = np.exp(b * theta1) * a

theta3 = np.linspace(np.pi, 0, 1000)
r3 = r1[-1] * np.ones_like(theta3)

theta4 = np.linspace(np.pi, 2 * np.pi, 1000)
r4 = a * np.ones_like(theta4)

theta5 = np.linspace(np.pi, 2 * np.pi, 1000)
r5 = r1[-1] * np.ones_like(theta5)

theta6 = np.linspace(0, np.pi, 1000)
r6 = a * np.ones_like(theta6)

# Concatenate pieces for filling
theta_final_red = np.concatenate([theta1, theta3, np.flip(theta2), theta4])
radius_red = np.concatenate([r1, r3, np.flip(r2), r4])

theta_final_blue = np.concatenate([theta1, theta5, np.flip(theta2), theta6])
radius_blue = np.concatenate([r1, r5, np.flip(r2), r6])

# Plot the filled spirals
fig = plt.figure(figsize=(7,4))
ax = fig.add_subplot(111, projection='polar')
ax.set_rmax(r1[-1])
ax.fill(theta_final_red, radius_red, "g")
ax.fill(theta_final_blue, radius_blue, "r")

# Plot the individual pieces
ax.plot(theta1, r1)
ax.plot(theta2, r2)

# Black inner circle
theta_inner = np.linspace(0, np.pi * 2.0, 1000, endpoint=True)
r_inner = [a] * len(theta_inner)
ax.fill(theta_inner, r_inner, c='black')

ax.axis(False)
ax.grid(False)

# Display the plot
plt.show()

输出

执行上述代码后，我们将获得以下输出：