
- 数字电子教程
- 数字电子 - 首页
- 数字电子基础
- 数字系统类型
- 信号类型
- 逻辑电平和脉冲波形
- 数字系统组件
- 数字逻辑运算
- 数字系统优势
- 数制
- 数制
- 二进制数表示
- 二进制运算
- 带符号二进制运算
- 八进制运算
- 十六进制运算
- 补码运算
- 进制转换
- 进制转换
- 二进制转十进制
- 十进制转二进制
- 二进制转八进制
- 八进制转二进制
- 八进制转十进制
- 十进制转八进制
- 十六进制转二进制
- 二进制转十六进制
- 十六进制转十进制
- 十进制转十六进制
- 八进制转十六进制
- 十六进制转八进制
- 二进制码
- 二进制码
- 8421 BCD码
- 余3码
- 格雷码
- ASCII码
- EBCDIC码
- 码转换
- 差错检测与纠错码
- 逻辑门
- 逻辑门
- 与门
- 或门
- 非门
- 通用门
- 异或门
- 异或非门
- CMOS逻辑门
- 使用二极管电阻逻辑的或门
- 与门与或门比较
- 二层逻辑实现
- 阈值逻辑
- 布尔代数
- 布尔代数
- 布尔代数定律
- 布尔函数
- 德摩根定理
- SOP和POS形式
- POS到标准POS形式
- 最小化技术
- 卡诺图最小化
- 三变量卡诺图
- 四变量卡诺图
- 五变量卡诺图
- 六变量卡诺图
- 无关项
- 奎因-麦克拉斯基方法
- 最小项和最大项
- 规范式和标准式
- 最大项表示
- 使用布尔代数化简
- 组合逻辑电路
- 数字组合电路
- 数字运算电路
- 多路复用器
- 多路复用器设计步骤
- 多路复用器通用门
- 使用4:1多路复用器的2变量函数
- 使用8:1多路复用器的3变量函数
- 多路分频器
- 多路复用器与多路分频器比较
- 奇偶校验位生成器和校验器
- 比较器
- 编码器
- 键盘编码器
- 优先编码器
- 译码器
- 算术逻辑单元
- 7段LED显示器
- 码转换器
- 码转换器
- 二进制转十进制转换器
- 十进制转BCD转换器
- BCD转十进制转换器
- 二进制转格雷码转换器
- 格雷码转二进制转换器
- BCD转余3码转换器
- 余3码转BCD转换器
- 加法器
- 半加器
- 全加器
- 串行加法器
- 并行加法器
- 使用半加器的全加器
- 半加器与全加器比较
- 使用与非门的全加器
- 使用与非门的半加器
- 二进制加减法器
- 减法器
- 半减器
- 全减器
- 并行减法器
- 使用两个半减器的全减器
- 使用与非门的半减器
- 时序逻辑电路
- 数字时序电路
- 时钟信号和触发
- 锁存器
- 移位寄存器
- 移位寄存器应用
- 二进制寄存器
- 双向移位寄存器
- 计数器
- 二进制计数器
- 非二进制计数器
- 同步计数器设计
- 同步计数器与异步计数器比较
- 有限状态机
- 算法状态机
- 触发器
- 触发器
- 触发器转换
- D触发器
- JK触发器
- T触发器
- SR触发器
- 带时钟的SR触发器
- 无时钟SR触发器
- 带时钟的JK触发器
- JK触发器转T触发器
- SR触发器转JK触发器
- 触发方法:触发器
- 边沿触发触发器
- 主从JK触发器
- 竞争冒险现象
- A/D和D/A转换器
- 模数转换器
- 数模转换器
- 数模转换器和模数转换器IC
- 逻辑门的实现
- 用与非门实现非门
- 用与非门实现或门
- 用与非门实现与门
- 用与非门实现或非门
- 用与非门实现异或门
- 用与非门实现异或非门
- 用或非门实现非门
- 用或非门实现或门
- 用或非门实现与门
- 用或非门实现与非门
- 用或非门实现异或门
- 用或非门实现异或非门
- 使用CMOS的与非门/或非门
- 使用与非门的全减器
- 使用2:1多路复用器的与门
- 使用2:1多路复用器的或门
- 使用2:1多路复用器的非门
- 存储器件
- 存储器件
- RAM和ROM
- 高速缓存设计
- 可编程逻辑器件
- 可编程逻辑器件
- 可编程逻辑阵列
- 可编程阵列逻辑
- 现场可编程门阵列
- 数字电子系列
- 数字电子系列
- CPU架构
- CPU架构
- 数字电子资源
- 数字电子 - 快速指南
- 数字电子 - 资源
- 数字电子 - 讨论
SR触发器转换为JK触发器
什么是SR触发器?
SR触发器 是一种简单的1位存储单元,它有两个输入,分别为S和R,以及两个输出,即Q和Q'。其中,S表示置位输入,R表示复位输入。输出Q是正常的输出,Q'是反相输出。除了SR输入外,SR触发器还有一个时钟输入,用于触发电路。
SR触发器的框图如下面的图1所示。
SR触发器的操作可以使用它的真值表进行分析,真值表如下所示。
| 输入 | 输出 | |
|---|---|---|
| S | R | Qn+1 |
| 0 | 0 | Qn |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 禁止 |
这里,Qn+1是下一个状态,Qn是输出的当前状态。
SR触发器的特性方程为:
$$\mathrm{Q_{n+1} \: = \: S+R'Q_{n}}$$
什么是JK触发器?
JK触发器 也是一个1位存储器件,它有两个输入,类似于SR触发器,但它的输入用J和K表示,而不是S和R。它有两个输出,即Q(正常输出)和Q'(反相输出)。时钟信号用于电路同步。
JK触发器的框图如下面的图2所示。
JK触发器的操作可以使用它的真值表来理解,真值表如下所示:
| 输入 | 输出 | |
|---|---|---|
| J | K | Qn+1 |
| 0 | 0 | Qn |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 翻转 |
JK触发器的特性方程为:
$$\mathrm{Q_{n+1}=JQ_{n}'+K'Q_{n}}$$
在讨论了SR触发器和JK触发器的基础知识之后。现在让我们讨论如何将SR触发器转换为JK触发器。
触发器转换
我们可以将一种类型的触发器转换为另一种类型的触发器。触发器的转换过程包括以下步骤:
步骤1 - 写出触发器的激励表。
步骤2 - 使用卡诺图(K-map)简化激励表。
步骤3 - 绘制所需的逻辑电路图。
现在,让我们将SR触发器转换为JK触发器。
将SR触发器转换为JK触发器
根据触发器转换步骤,将SR触发器转换为JK触发器的转换过程如下所述。
步骤1 - 将SR触发器转换为JK触发器的激励表如下所示:
| 输入 | 输出的当前状态 | 输出的下一个状态 | 触发器输入 | ||||
|---|---|---|---|---|---|---|---|
| J | K | Qn | Qn+1 | S | R | S | R |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | X |
| 0 | 1 | ||||||
| 0 | 0 | 1 | 1 | 0 | 0 | X | 0 |
| 1 | 0 | ||||||
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | X |
| 0 | 1 | ||||||
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | X | 0 |
| 1 | 0 | ||||||
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
步骤2 - 使用K-Map简化输入表达式的激励:
S的K-Map简化是:
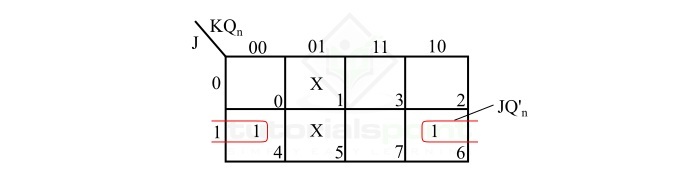
S = JQn'
R的K-Map简化是:
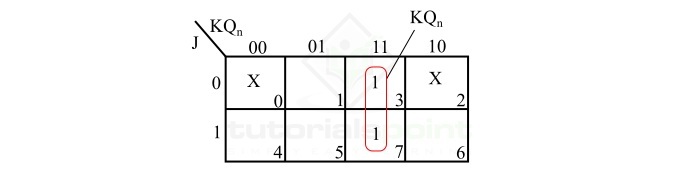
R = KQn
步骤3 - 最后,使用SR触发器绘制JK触发器的逻辑图,如下面的图3所示。
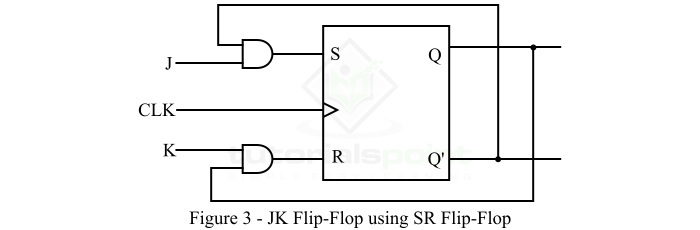
这样,我们就可以将SR触发器转换为JK触发器了。