数字电子学 - 二进制码

---

---

二进制码是数字电子学中的一个重要概念。二进制码是一种数字代码，由两个数字0和1组成。二进制码是任何数字计算系统的主要语言。二进制码可以表示不同类型的信息，例如数字、字母、图像、视频等。

在本章中，我们将解释二进制码的基础知识、工作原理、优点、局限性和应用。

什么是二进制码？

二进制码用于以0和1（即二进制数字）的形式表示文本、数字、图像或其他类型的信息。二进制码构成计算机等数字计算系统的主要语言。

所有数字系统只能理解和处理以二进制语言表示的信息。在二进制码中，每个数字称为二进制数字或位。

二进制码使用0和1表示信息。在数字系统中，二进制码被组织成段，例如位或字节。位是二进制的0或1。当8位组合在一起时，它被称为字节。每个字节在数字系统中表示一段信息。

二进制码的类型

二进制码可以分为以下主要类型：

• 加权二进制码
• 非加权二进制码
• 字母数字码
• 二进制编码的十进制 (BCD)
• 错误检测码
• 纠错码

让我们详细讨论每种代码类型。

加权二进制码

加权二进制码是一种二进制码，其中每个位位置都与其位置值相关联的特定权重。

在加权二进制码中，位置权重以2的幂来定义。每个位的值取决于其在二进制码中的位置。因此，在给定的加权二进制码中，最右边的位具有最小的权重，而最左边的位具有最大的权重。

一般来说，加权二进制码中第n位的权重由下式给出：

第n位 = 2ⁿ

例如，设一个4位加权二进制码1011。该代码的值为：

1 × 2³ + 0 × 2² + 1 × 2¹ + 1 × 2⁰

1 × 8 + 0 × 4 + 1 × 2 + 1 × 1

8 + 0 + 2 + 1 = 11

很明显，最右边的位的位置权重为2⁰ = 1，而最左边的位的位置权重为2³ = 8。

加权二进制码的例子有8421 BCD码、5211码、2421码等。

非加权二进制码

在数字电子学中，每一位位置都没有与其相关联的特定权重的数字或二进制码类型称为非加权二进制码。

在非加权二进制码中，位的值不取决于其在数字中的位置。每个位位置具有相同的位置值。

非加权二进制码的例子包括余3码和格雷码。

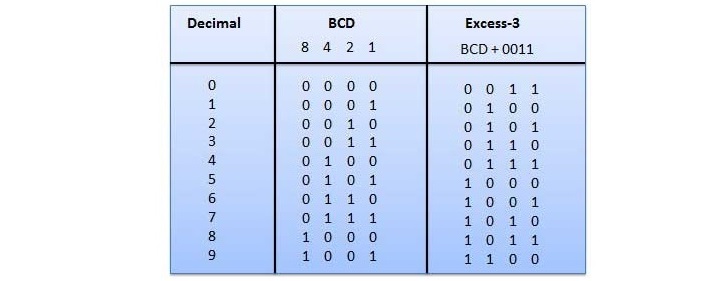
余3码

余3码也称为XS-3码。它是一种非加权码，用于表示十进制数。余3码字是通过将(0011)₂或(3)₁₀添加到8421 BCD码字的每个码字中而导出的。

余3码的获得方法如下：

看下面的例子：

格雷码

格雷码是一种非加权码。它们不是算术码，这意味着没有为位位置分配特定的权重。

格雷码有一个非常特殊的特性，即每次十进制数递增时，只有一位会改变（见下图）。因为一次只改变一位，所以格雷码也被称为单位距离码。

格雷码是循环码，不能用于算术运算。

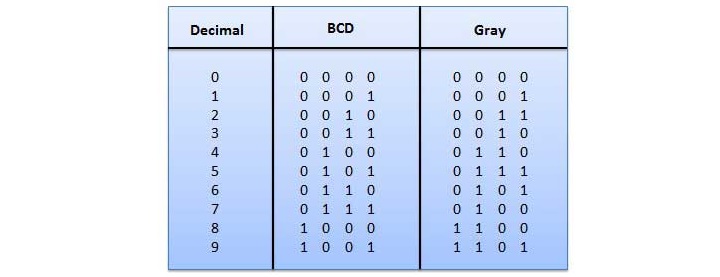
格雷码广泛应用于轴位置编码器。轴位置编码器产生一个代码字，表示轴的角位置。

字母数字码

一个二进制数字或位只能表示两种状态“0”或“1”。但这对于两台计算机之间的通信来说是不够的，因为我们需要更多符号进行通信。这些符号需要表示26个大写和小写字母、0到9的数字、标点符号和其他符号。

字母数字码是表示数字和字母字符的代码。大多数此类代码还表示其他字符，例如符号和传送信息所需的各种指令。

字母数字码是使用字符编码方案表示数字和字母字符的二进制码。字母数字码主要用于涉及字符表示和信息交换的应用程序。

一些常见的字母数字码示例包括ASCII（美国信息交换标准代码）、扩展ASCII、EBCDIC（扩展二进制编码的十进制交换代码）、Unicode等。

字母数字码至少应表示10个数字和26个字母，即总共36个项目。以下三个字母数字码非常常用地用于数据表示：

• 美国信息交换标准代码 (ASCII)
• 扩展二进制编码的十进制交换代码 (EBCDIC)
• 五位鲍多码

ASCII码是7位码，而EBCDIC是8位码。ASCII码更常用，而EBCDIC主要用于大型IBM计算机。

二进制编码的十进制 (BCD)

二进制编码的十进制或BCD是一种二进制码，用于以数字格式表示十进制数。在这种代码中，每个十进制数字都由一个4位二进制数表示。BCD是一种用二进制代码表示每个十进制数字的方法。在BCD中，每个十进制数字都由二进制位的唯一组合表示。

BCD主要用于执行十进制算术运算的数字系统，例如计算机、计算器、显示设备、数字传感器等。

在BCD中，用4位可以表示十六个数（0000到1111），但在BCD码中只使用了前十个（0000到1001）。其余六个代码组合，即1010到1111在BCD中无效。

BCD码的优点

• BCD码与十进制系统非常相似。
• 我们只需要记住0到9的十进制数的二进制等价物。

BCD码的缺点

• BCD码的加法和减法遵循不同的规则。
• BCD算术稍微复杂一些。
• BCD表示十进制数所需的位数比二进制多。因此，BCD的效率低于二进制。

错误检测码

检错码是特殊的二进制码，用于识别数字通信和数据存储中的错误。检错码向数据添加冗余信息，允许接收方识别是否发生了错误。常见的检错码包括奇偶校验位、校验和、汉明码等。

检错码对于确保数据传输和存储的完整性非常重要。它们有助于提高系统的可靠性。

什么是错误？

错误是指输出信息与输入信息不匹配的情况。在传输过程中，数字信号会受到噪声的影响，这可能会在从一个系统到另一个系统的二进制位传输过程中引入错误。这意味着 0 位可能会变为 1，或者 1 位可能会变为 0。

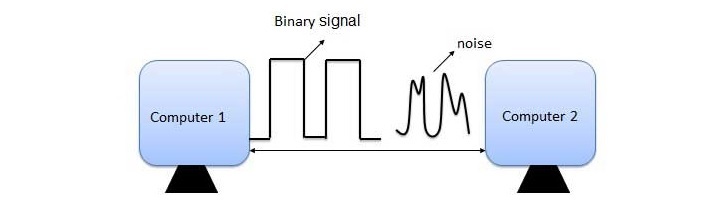
每当传输消息时，它都可能被噪声扰乱，或者数据可能被损坏。为避免这种情况，我们使用检错码，即添加到给定数字消息中的附加数据，以帮助我们检测消息传输过程中是否发生错误。检错码的一个简单示例是奇偶校验。

纠错码

纠错码是二进制码，旨在纠正数字系统在数据传输或存储过程中发生的错误。纠错码向要传输或存储的数据添加一些附加信息。

纠错码采用与检错码相同的策略，但此外，此类代码还可以检测损坏位的精确位置。这允许接收方即使某些位损坏也能重新获取原始数据。

在纠错码中，奇偶校验有一种简单的方法来检测错误，以及一种复杂的机制来确定损坏位的位置。一旦找到损坏位，就会将其值反转（从 0 变为 1 或从 1 变为 0）以获取原始消息。

与检错码一样，纠错码对于维护数字通信和数据存储应用程序中的数据完整性也很重要。

不同的数字系统根据通信信道类型、错误模式、纠错程度等使用不同类型的纠错码。一些常见的纠错码示例包括汉明码、里德-所罗门码、低密度奇偶校验码、BCH 码等。

如何检测和纠正错误？

为了检测和纠正错误，在传输时会向数据位添加附加位。

• 附加位称为奇偶校验位。它们允许检测或纠正错误。
• 数据位和奇偶校验位一起构成一个码字。

奇偶校验检错

这是检测和纠正错误最简单的技术。8 位字的 MSB 用作奇偶校验位，其余 7 位用作数据位或消息位。8 位传输字的奇偶校验可以是偶校验或奇校验。

偶校验 - 偶校验意味着给定字中包括奇偶校验位在内的 1 的数量应为偶数 (2,4,6,……)。

奇校验 - 奇校验意味着给定字中包括奇偶校验位在内的 1 的数量应为奇数 (1,3,5,……)。

奇偶校验位的用法

根据所需的奇偶校验类型，可以将奇偶校验位设置为“0”或“1”。

对于偶校验，此位设置为 1 或 0，以使整个字中“1 位”的数量为偶数。参见图 (a)。

对于奇校验，此位设置为 1 或 0，以使整个字中“1 位”的数量为奇数。参见图 (b)。

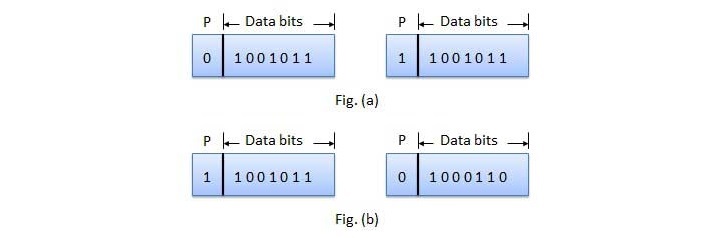
错误检测是如何进行的？

如果接收信号的奇偶校验与预期奇偶校验不同，则接收端的奇偶校验可以检测到错误的存在。这意味着，如果已知传输信号的奇偶校验始终为“偶”，而接收信号具有奇校验，则接收方可以得出结论：接收信号不正确。

如果检测到错误，则接收方将忽略接收到的字节，并请求向发送方重新传输相同的字节。

二进制码的优点

二进制码在数字电子领域具有多种优势。以下是使用二进制码的主要好处：

• 简单性 - 二进制码仅使用两个数字，即 0 和 1 来表示信息。它简化了电子电路的设计和实现。
• 易于实现 - 二进制码仅使用两种状态，即开和关。因此，它们的实现非常简单。
• 易于存储 - 二进制码易于存储在数字存储设备中，如硬盘、CD、DVD、U 盘等。它们需要更高效的紧凑存储。
• 易于快速处理 - 具有算术逻辑单元的数字系统可以有效地处理二进制码。它们允许快速且无错误的计算。
• 易于通信 - 二进制码提供了一种以非常高的速度有效传输信息的方法。可以将各种检错和纠错技术应用于二进制码，从而使数字通信更有效。
• 易于扩展 - 二进制码提供了数字系统的易于扩展性。我们只需在代码中添加更多位即可增加数字系统的范围。
• 兼容性 - 二进制码与各种数字设备和系统兼容。
• 可靠性 - 二进制码对噪声和干扰具有很强的免疫力，这提高了数字系统的可靠性。

二进制码的缺点

二进制码具有上述多种优点。但是，它们也有一些缺点和局限性。

下面列出了一些二进制码的主要缺点：

• 二进制码不方便人类使用。对于人类来说，阅读和解释二进制码可能是一项复杂的任务。
• 在某些情况下，必须将二进制码转换为其他数字系统，这会增加系统的额外计算开销。
• 二进制码需要在通信信道中更高的传输带宽。
• 在二进制码中，识别错误相当困难。在较长的二进制序列的情况下，这变得更具挑战性。

二进制码的应用

由于二进制码在信息表示方面的高效率，因此广泛应用于数字电子的各个领域。

下面列出了一些二进制码的关键应用：

• 数字计算机 - 二进制码主要用于数字计算机中表示信息和指令。
• 数字通信 - 二进制码也用于使用数字信道传输数据和信息。
• 数字显示 - 二进制码也用于在数字系统中显示数字和字母。
• 条形码系统 - 二进制码也用于条形码系统中进行产品识别和库存管理。在这个系统中，不同宽度和之间间隔的条形代表二进制数字，扫描器可以解释这些数字。
• 数据存储 - 二进制码用于存储数字设备（如计算机内存）中的信息。
• 数字控制系统 - 二进制码用于编程数字控制系统。在数字控制系统中，二进制码用于表示用于自动化的不同类型的控制信号和指令。
• 计算机图形学 - 二进制码也用于计算机图形学中表示颜色、形状、像素值和其他信息。

结论

总之，二进制码是数字系统的重要组成部分之一。它们用于以数字格式表示信息和指令。数字电子中使用了多种不同类型的二进制码。

根据应用的性质，不同的二进制码用于不同的目的。例如，ASCII 码用于字母数字数据表示。在本节中，我们解释了二进制码的基本概念。在接下来的章节中，我们将探讨不同类型的二进制码及其在数字电子中的应用。