
- 数字电子学教程
- 数字电子学 - 首页
- 数字电子学基础
- 数字系统类型
- 信号类型
- 逻辑电平和脉冲波形
- 数字系统组件
- 数字逻辑运算
- 数字系统优势
- 数制
- 数制
- 二进制数表示
- 二进制算术
- 有符号二进制算术
- 八进制算术
- 十六进制算术
- 补码算术
- 进制转换
- 进制转换
- 二进制到十进制转换
- 十进制到二进制转换
- 二进制到八进制转换
- 八进制到二进制转换
- 八进制到十进制转换
- 十进制到八进制转换
- 十六进制到二进制转换
- 二进制到十六进制转换
- 十六进制到十进制转换
- 十进制到十六进制转换
- 八进制到十六进制转换
- 十六进制到八进制转换
- 二进制编码
- 二进制编码
- 8421 BCD码
- 余3码
- 格雷码
- ASCII码
- EBCDIC码
- 编码转换
- 错误检测和纠错码
- 逻辑门
- 逻辑门
- 与门
- 或门
- 非门
- 通用门
- 异或门
- 异或非门
- CMOS逻辑门
- 使用二极管电阻逻辑的或门
- 与门与或门
- 双电平逻辑实现
- 阈值逻辑
- 布尔代数
- 布尔代数
- 布尔代数定律
- 布尔函数
- 德摩根定理
- SOP和POS形式
- POS到标准POS形式
- 最小化技术
- 卡诺图最小化
- 三变量卡诺图
- 四变量卡诺图
- 五变量卡诺图
- 六变量卡诺图
- 无关项条件
- 奎因-麦克斯韦尔方法
- 最小项和最大项
- 规范式和标准式
- 最大项表示
- 使用布尔代数化简
- 组合逻辑电路
- 数字组合电路
- 数字算术电路
- 多路复用器
- 多路复用器设计流程
- MUX通用门
- 使用4:1 MUX的2变量函数
- 使用8:1 MUX的3变量函数
- 多路分解器
- MUX与DEMUX
- 奇偶校验位生成器和校验器
- 比较器
- 编码器
- 键盘编码器
- 优先编码器
- 译码器
- 算术逻辑单元
- 7段LED显示器
- 代码转换器
- 代码转换器
- 二进制到十进制转换器
- 十进制到BCD转换器
- BCD到十进制转换器
- 二进制到格雷码转换器
- 格雷码到二进制转换器
- BCD到余3码转换器
- 余3码到BCD转换器
- 加法器
- 半加器
- 全加器
- 串行加法器
- 并行加法器
- 使用半加器的全加器
- 半加器与全加器
- 使用与非门的全加器
- 使用与非门的半加器
- 二进制加法/减法器
- 减法器
- 半减器
- 全减器
- 并行减法器
- 使用2个半减器的全减器
- 使用与非门的半减器
- 时序逻辑电路
- 数字时序电路
- 时钟信号和触发
- 锁存器
- 移位寄存器
- 移位寄存器应用
- 二进制寄存器
- 双向移位寄存器
- 计数器
- 二进制计数器
- 非二进制计数器
- 同步计数器设计
- 同步计数器与异步计数器
- 有限状态机
- 算法状态机
- 触发器
- 触发器
- 触发器转换
- D触发器
- JK触发器
- T触发器
- SR触发器
- 带时钟的SR触发器
- 无时钟的SR触发器
- 带时钟的JK触发器
- JK到T触发器
- SR到JK触发器
- 触发方式:触发器
- 边沿触发触发器
- 主从JK触发器
- 竞争冒险现象
- A/D和D/A转换器
- 模数转换器
- 数模转换器
- DAC和ADC集成电路
- 逻辑门的实现
- 使用与非门实现非门
- 使用与非门实现或门
- 使用与非门实现与门
- 使用与非门实现或非门
- 使用与非门实现异或门
- 使用与非门实现异或非门
- 使用或非门实现非门
- 使用或非门实现或门
- 使用或非门实现与门
- 使用或非门实现与非门
- 使用或非门实现异或门
- 使用或非门实现异或非门
- 使用CMOS的与非/或非门
- 使用与非门实现全减器
- 使用2:1 MUX实现与门
- 使用2:1 MUX实现或门
- 使用2:1 MUX实现非门
- 存储器件
- 存储器件
- RAM和ROM
- 缓存存储器设计
- 可编程逻辑器件
- 可编程逻辑器件
- 可编程逻辑阵列
- 可编程阵列逻辑
- 现场可编程门阵列
- 数字电子学系列
- 数字电子学系列
- CPU架构
- CPU架构
- 数字电子学资源
- 数字电子学 - 快速指南
- 数字电子学 - 资源
- 数字电子学 - 讨论
数字电子学 - N位并行加法器
让我们从简要介绍二进制加法器和二进制加法的规则开始本文。在数字电子学中,加法器或二进制加法器是一种组合数字电路,用于执行两个或多个二进制数字的加法运算。两个位的二进制加法是按照以下四个规则执行的:
$$\mathrm{0 \: + \: 0 \: = \: 0}$$
$$\mathrm{0 \: + \: 1 \: = \: 1}$$
$$\mathrm{1 \: + \: 0 \: = \: 1}$$
$$\mathrm{1 \: + \: 1 \: = \: 10 (和 \: = \: 0; 进位 \: = \: 1)}$$
前三个运算产生的和的位长度为一位二进制数字。但是,最后一个组合的和,即当被加数和加数都等于1时,二进制和由两位二进制数字组成,即和位和进位位。最高有效位是进位位,而最低有效位是和位。
为了更好地理解N位并行加法器的实现和操作,我们还需要了解全加器电路。下面将介绍全加器及其框图和真值表。
什么是全加器?
一个组合数字电路,它将两个位和一个进位位相加,并产生一个和位和一个进位位作为输出,被称为全加器(FA)。
换句话说,一个可以将三个输入位相加并产生两个输出位(即和位和进位位)的二进制加法器电路称为全加器。全加器的框图如图1所示。
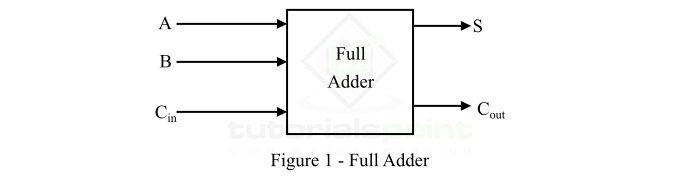
这里,A和B是输入位,Cin是来自前一个和的输入进位位,S是输出和位,Cout是输出进位位。
从全加器电路的真值表可以很容易地理解其工作原理,如下所示。
| 输入 | 输出 | |||
|---|---|---|---|---|
| A | B | Cin | S | Cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
现在,让我们讨论一下如何使用全加器实现N位并行加法器。
N位并行加法器
并行加法器是一种二进制加法器电路,用于添加具有N位(例如,要添加4位二进制数,我们使用4位并行加法器,依此类推)的两个二进制数。顾名思义,并行加法器是一种数字组合电路,它并行地添加两个二进制数,并并行地生成这些二进制数的算术和。
正如我们上面已经提到的,全加器只能执行由两个输入位和一个输入进位位组成的两个一位二进制数的加法运算,即三个位的加法运算。但在实际应用中,我们必须添加位数大于一位的二进制数。为了添加此类二进制数,我们使用并行二进制加法器,它能够添加任何位长的两个二进制数,例如4位、5位等。
我们可以借助以链式方式连接的全加器来实现N位并行加法器。图2显示了使用全加器的N位并行加法器的框图表示。
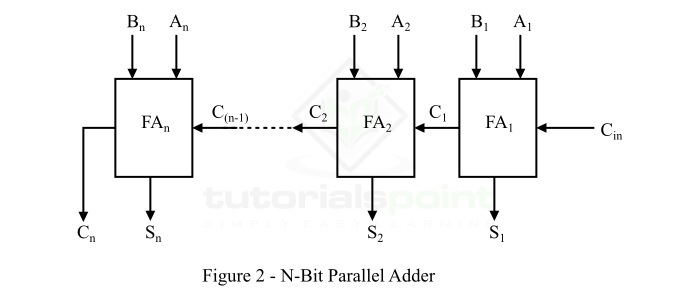
从N位并行加法器的框图可以看出,每个全加器的进位输出连接到链中下一个更高级别的全加器的进位输入端。
要实现并行加法器,所需的全加器数量由要相加的两个二进制数的位数决定。因此,一个N位并行加法器需要N个全加器来并行地执行加法运算。例如,一个2位并行加法器需要2个全加器,一个4位并行加法器由4个全加器组成,依此类推。
N位并行加法器电路的工作原理
图2所示的N位并行加法器的工作原理可以描述如下步骤:
- 最初,全加器FA1将两个输入位A1和B1以及一个输入进位位Cin相加,并生成输出和位S1和进位位C1,进位位C1被转发到链中的下一个加法器(FA2)。和位S1是输出和的最低有效位。
- 在下一阶段,全加器电路FA2被激活,并将输入位A2和B2以及C1相加。它生成和位S2,它是输出和的第二位,以及进位位C2,进位位C2连接到链中的下一个全加器FA3。
- 此过程将持续到链中的最后一个全加器,即FAn。全加器使用进位输入C(n-1)与输入位An和Bn相加,以产生输出和的最后一位Sn和最后的输出进位位Cn。
并行加法器的优点
并行加法器的一些重要优点如下:
- 并行加法器同时添加位。
- 它使二进制数的加法运算更快。
- 并行加法器更经济。
并行加法器的缺点
并行加法器的主要缺点是传播延迟。因为,在并行加法器中,来自先前加法的进位必须传播到下一个加法器,这需要一些时间。这会导致加法运算中出现明显的传播延迟。这种传播延迟与二进制数的位数成正比。
并行加法器的应用
并行加法器的重要应用如下:
- 并行加法器用于算术逻辑单元,而算术逻辑单元则用于高性能计算应用。
- 并行加法器也用于并行细胞自动机进行并行计算。
- 并行加法器用于将BCD码转换为余3码。
- 并行加法器还用于分析乘法算法。
结论
我们可以得出结论,n位并行加法器是一种组合数字电路,它使用n个全加器来并行地对两个二进制数进行加法运算。并行加法器同时执行各位的加法,因此它提高了二进制加法的速度。