两级逻辑实现

---

---

在两级逻辑中，输入和输出之间存在的最大级数为两级。这意味着，无论逻辑门的总数是多少，在任何输入和输出之间存在的（级联）逻辑门的最大数量在两级逻辑中为两级。这里，第一级逻辑门的输出连接作为第二级逻辑门(s)的输入。

考虑四个逻辑门：与门、或门、与非门和或非门。由于有4个逻辑门，我们将得到16种实现两级逻辑的可能方法。它们是与-与、与-或、与-与非、与-或非、或-与、或-或、或-与非、或-或非、与非-与、与非-或、与非-与非、与非-或非、或非-与、或非-或、或非-与非、或非-或非。

这些两级逻辑实现可以分为以下两类。

• 退化形式
• 非退化形式

退化形式

如果两级逻辑实现的输出可以使用单个逻辑门获得，则称为退化形式。显然，单个逻辑门的输入数量会增加。因此，逻辑门的扇入增加。这是退化形式的一个优点。

在16种组合中，只有6种两级逻辑实现组合属于退化形式。它们是与-与、与-与非、或-或、或-或非、与非-或非、或非-与非。

在本节中，让我们讨论一些实现。假设A、B、C和D是输入，Y是每个逻辑实现中的输出。

与-与逻辑

在这种逻辑实现中，两级都存在与门。下图显示了与-与逻辑实现的一个示例。

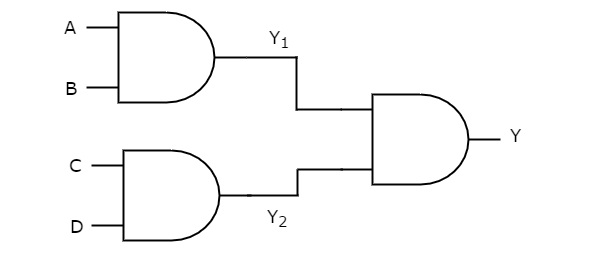
我们将得到第一级逻辑门的输出为Y₁ = AB和Y₂ = CD

这些输出Y₁和Y₂作为第二级存在的与门的输入。因此，该与门的输出为

$$\mathrm{Y\:=\:Y_{1}Y_{2}}$$

将Y₁和Y₂的值代入上式。

$$\mathrm{Y \: = \: (AB)(CD)}$$

$$\mathrm{\Rightarrow \: Y \: = \: ABCD}$$

因此，这种与-与逻辑实现的输出为ABCD。此布尔函数可以使用4输入与门实现。因此，它是退化形式。

与-与非逻辑

在这种逻辑实现中，第一级存在与门，第二级存在与非门(s)。下图显示了与-与非逻辑实现的一个示例。

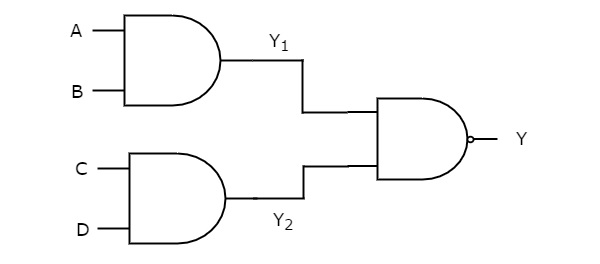
之前，我们得到第一级逻辑门的输出为Y₁ = AB和Y₂ = CD

这些输出Y₁和Y₂作为第二级存在的与非门的输入。因此，该与非门的输出为

$$\mathrm{Y \: = \:(Y_{1}Y_{2})'}$$

将Y₁和Y₂的值代入上式。

$$\mathrm{Y \: = \: ((AB)(CD))'}$$

$$\mathrm{\Rightarrow \: Y \: = \: (ABCD)'}$$

因此，这种与-与非逻辑实现的输出为(ABCD)'。此布尔函数可以使用4输入与非门实现。因此，它是退化形式。

或-或逻辑

在这种逻辑实现中，两级都存在或门。下图显示了或-或逻辑实现的一个示例。

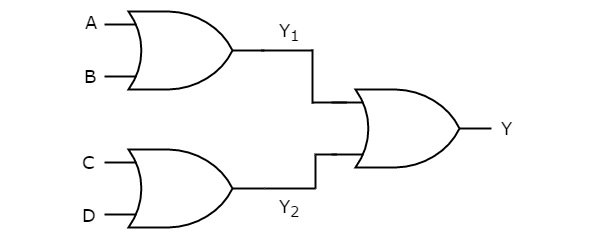
我们将得到第一级逻辑门的输出为Y₁ = A + B和Y₂ = C + D。

这些输出Y₁和Y₂作为第二级存在的或门的输入。因此，该或门的输出为

$$\mathrm{Y \:= \: Y_{1}\:+\:Y_{2}}$$

将Y₁和Y₂的值代入上式。

$$\mathrm{Y \: = \: (A\:+\:B) \: + \: (C\:+\:D)}$$

$$\mathrm{\Rightarrow \: Y \:=\:A\:+\:B\:+\:C\:+\:D}$$

因此，这种或-或逻辑实现的输出为A + B + C + D。此布尔函数可以使用4输入或门实现。因此，它是退化形式。

类似地，您可以验证其余实现是否属于此类别。

非退化形式

如果两级逻辑实现的输出不能使用单个逻辑门获得，则称为非退化形式。

其余10种两级逻辑实现组合属于非退化形式。它们是与-或、与-或非、或-与、或-与非、与非-与、与非-或、与非-与非、或非-与、或非-或、或非-或非。

现在，让我们讨论一些实现。假设A、B、C和D是输入，Y是每个逻辑实现中的输出。

与-或逻辑

在这种逻辑实现中，第一级存在与门，第二级存在或门(s)。下图显示了与-或逻辑实现的一个示例。

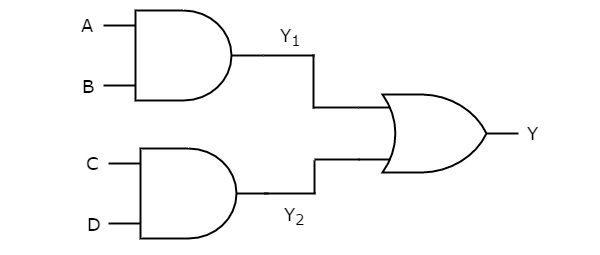
之前，我们得到第一级逻辑门的输出为Y₁ = AB和Y₂ = CD。

这些输出Y₁和Y₂作为第二级存在的或门的输入。因此，该或门的输出为

$$\mathrm{Y\:=\:Y_{1}\:+\:Y_{2}}$$

将Y₁和Y₂的值代入上式

$$\mathrm{Y\:=\:AB\:+\:CD}$$

因此，这种与-或逻辑实现的输出为AB + CD。此布尔函数采用积之和形式。由于我们无法使用单个逻辑门实现它，因此这种与-或逻辑实现是一种非退化形式。

与-或非逻辑

在这种逻辑实现中，第一级存在与门，第二级存在或非门(s)。下图显示了与-或非逻辑实现的一个示例。

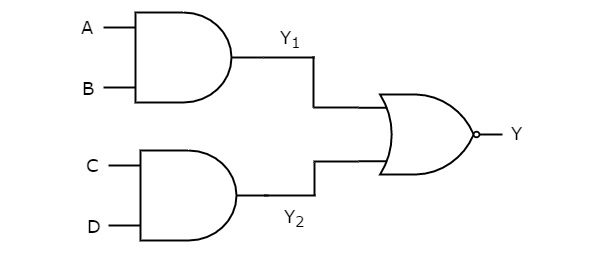
我们知道第一级逻辑门的输出为Y₁ = AB和Y₂ = CD

这些输出Y₁和Y₂作为第二级存在的或非门的输入。因此，该或非门的输出为

$$\mathrm{Y \:=\:(Y_{1}\:+\:Y_{2})'}$$

将Y₁和Y₂的值代入上式。

$$\mathrm{Y\:=\:(AB\:+\:CD)'}$$

因此，这种与-或非逻辑实现的输出为(AB + CD)'。此布尔函数采用与-或-非形式。由于我们无法使用单个逻辑门实现它，因此这种与-或非逻辑实现是一种非退化形式

或-与逻辑

在这种逻辑实现中，第一级存在或门，第二级存在与门(s)。下图显示了或-与逻辑实现的一个示例。

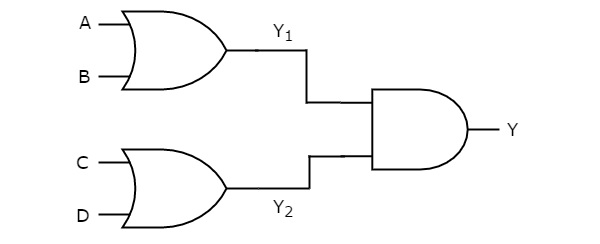
之前，我们得到第一级逻辑门的输出为Y₁ = A + B和Y₂ = C + D。

这些输出Y₁和Y₂作为第二级存在的与门的输入。因此，该与门的输出为

$$\mathrm{Y\:=\:Y_{1}Y_{2}}$$

将Y₁和Y₂的值代入上式。

$$\mathrm{Y \: = \: (A\:+\:B)(C\:+\:D)}$$

因此，这种或-与逻辑实现的输出为(A + B)(C + D)。此布尔函数采用和之积形式。由于我们无法使用单个逻辑门实现它，因此这种或-与逻辑实现是一种非退化形式。

类似地，您可以验证其余实现是否属于此类别。