
- 数字电子教程
- 数字电子 - 首页
- 数字电子基础
- 数字系统的类型
- 信号的类型
- 逻辑电平和脉冲波形
- 数字系统组件
- 数字逻辑运算
- 数字系统优势
- 数制
- 数制
- 二进制数表示
- 二进制运算
- 带符号二进制运算
- 八进制运算
- 十六进制运算
- 补码运算
- 进制转换
- 进制转换
- 二进制到十进制转换
- 十进制到二进制转换
- 二进制到八进制转换
- 八进制到二进制转换
- 八进制到十进制转换
- 十进制到八进制转换
- 十六进制到二进制转换
- 二进制到十六进制转换
- 十六进制到十进制转换
- 十进制到十六进制转换
- 八进制到十六进制转换
- 十六进制到八进制转换
- 二进制代码
- 二进制代码
- 8421 BCD码
- 余3码
- 格雷码
- ASCII码
- EBCDIC码
- 代码转换
- 错误检测与纠错码
- 逻辑门
- 逻辑门
- 与门
- 或门
- 非门
- 通用门
- 异或门
- 异或非门
- CMOS逻辑门
- 使用二极管电阻逻辑的或门
- 与门与或门
- 两级逻辑实现
- 阈值逻辑
- 布尔代数
- 布尔代数
- 布尔代数定律
- 布尔函数
- 德摩根定理
- SOP和POS形式
- POS到标准POS形式
- 最小化技术
- 卡诺图最小化
- 三变量卡诺图
- 四变量卡诺图
- 五变量卡诺图
- 六变量卡诺图
- 无关项条件
- 奎因-麦克拉斯基方法
- 最小项和最大项
- 规范形式和标准形式
- 最大项表示
- 使用布尔代数进行简化
- 组合逻辑电路
- 数字组合电路
- 数字算术电路
- 多路复用器
- 多路复用器设计过程
- 多路复用器通用门
- 使用4:1多路复用器的2变量函数
- 使用8:1多路复用器的3变量函数
- 多路分解器
- 多路复用器与多路分解器
- 奇偶校验位生成器和校验器
- 比较器
- 编码器
- 键盘编码器
- 优先编码器
- 解码器
- 算术逻辑单元
- 7段LED显示器
- 代码转换器
- 代码转换器
- 二进制到十进制转换器
- 十进制到BCD转换器
- BCD到十进制转换器
- 二进制到格雷码转换器
- 格雷码到二进制转换器
- BCD到余3码转换器
- 余3码到BCD转换器
- 加法器
- 半加器
- 全加器
- 串行加法器
- 并行加法器
- 使用半加器的全加器
- 半加器与全加器
- 使用与非门的全加器
- 使用与非门的半加器
- 二进制加法器-减法器
- 减法器
- 半减器
- 全减器
- 并行减法器
- 使用2个半减器的全减器
- 使用与非门的半减器
- 时序逻辑电路
- 数字时序电路
- 时钟信号和触发
- 锁存器
- 移位寄存器
- 移位寄存器应用
- 二进制寄存器
- 双向移位寄存器
- 计数器
- 二进制计数器
- 非二进制计数器
- 同步计数器设计
- 同步计数器与异步计数器
- 有限状态机
- 算法状态机
- 触发器
- 触发器
- 触发器转换
- D触发器
- JK触发器
- T触发器
- SR触发器
- 带时钟的SR触发器
- 无时钟的SR触发器
- 带时钟的JK触发器
- JK到T触发器
- SR到JK触发器
- 触发方法:触发器
- 边沿触发触发器
- 主从JK触发器
- 竞争冒险现象
- A/D和D/A转换器
- 模数转换器
- 数模转换器
- DAC和ADC集成电路
- 逻辑门的实现
- 用与非门实现非门
- 用与非门实现或门
- 用与非门实现与门
- 用与非门实现或非门
- 用与非门实现异或门
- 用与非门实现异或非门
- 用或非门实现非门
- 用或非门实现或门
- 用或非门实现与门
- 用或非门实现与非门
- 用或非门实现异或门
- 用或非门实现异或非门
- 使用CMOS的与非/或非门
- 使用与非门的全减器
- 使用2:1多路复用器的与门
- 使用2:1多路复用器的或门
- 使用2:1多路复用器的非门
- 存储器件
- 存储器件
- RAM和ROM
- 高速缓存存储器设计
- 可编程逻辑器件
- 可编程逻辑器件
- 可编程逻辑阵列
- 可编程阵列逻辑
- 现场可编程门阵列
- 数字电子系列
- 数字电子系列
- CPU架构
- CPU架构
- 数字电子资源
- 数字电子 - 快速指南
- 数字电子 - 资源
- 数字电子 - 讨论
数字电子 - 解码器
什么是解码器?
在数字电子学中,一种组合逻辑电路,它将N位二进制输入代码转换为M个输出通道,使得对于每一种可能的输入组合,只有一个输出通道被激活,这种电路被称为解码器。
换句话说,一种将N条输入线转换为最多2N条输出线的组合逻辑电路称为解码器。
因此,解码器是一种能够识别或检测特定代码的组合逻辑电路。解码器执行的操作称为解码。解码器的通用框图如图1所示。
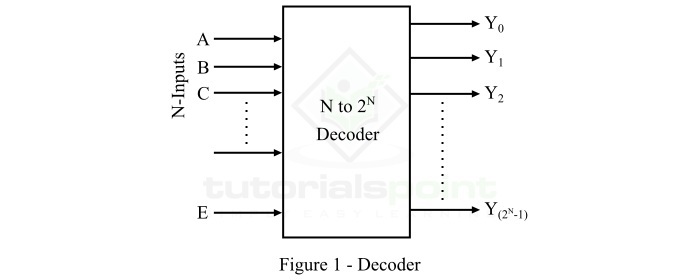
这里,解码器有N条输入线和M(2N)条输出线。在解码器中,每条输入线可以是0或1,因此可能的输入组合或代码的数量等于2N。对于这些输入组合中的每一个,只有M条输出线中的一条将被激活,而其他所有输出线将保持非激活状态。
解码器的类型
存在几种类型的解码器。但是,根据存在的输入和输出线,解码器可以分为以下三种类型:
- 2到4解码器
- 3到8解码器
- 4到16解码器
现在,让我们逐一详细讨论每种类型的解码器。
2到4解码器
2到4解码器是一种具有2条输入线和4(22)条输出线的解码器。2到4解码器的功能框图如图2所示。
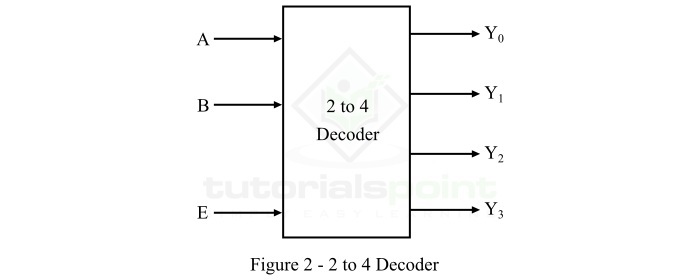
当使用使能输入E使该解码器启用时,则对于每种输入组合,其四个输出中的一个将被激活。可以使用下表给出的真值表来分析此2线到4线解码器的操作。
| 输入 | 输出 | |||||
|---|---|---|---|---|---|---|
| E | A | B | Y3 | Y2 | Y1 | Y0 |
| 0 | X | X | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
使用此真值表,我们可以导出每个输出的布尔表达式,如下所示:
$$\mathrm{Y_{0} \: = \: E \: \cdot \: \bar{A} \: \cdot \: \bar{B}}$$
$$\mathrm{Y_{1} \: = \: E \: \cdot \: \bar{A} \: \cdot \: B}$$
$$\mathrm{Y_{2} \: = \: E \: \cdot \: A \: \cdot \: \bar{B}}$$
$$\mathrm{Y_{3} \: = \: E \: \cdot \: A \: \cdot \: B}$$
由于每个输出项都包含输入变量的乘积,因此可以使用与门来实现。因此,2到4解码器的逻辑电路图如图3所示。
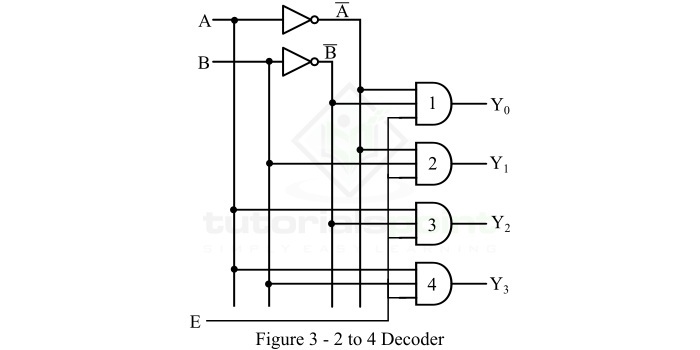
操作
2到4解码器逻辑电路的操作描述如下:
- 当使能输入(E)处于非活动状态,即设置为0时,任何与门都不会工作。
- 当使能输入(E)通过设置为1使其处于活动状态时,电路将按以下方式工作。
- 当A = 0且B = 0时,与门1被激活并产生输出Y0。
- 当A = 0且B = 1时,与门2被激活并产生输出Y1。
- 当A = 1且B = 0时,与门3被激活并产生输出Y2。
- 当A = 1且B = 1时,与门4被激活并产生输出Y3。
3到8解码器
3到8解码器是一种具有3条输入线和8(23)条输出线的解码器。3到8解码器的功能框图如图4所示。
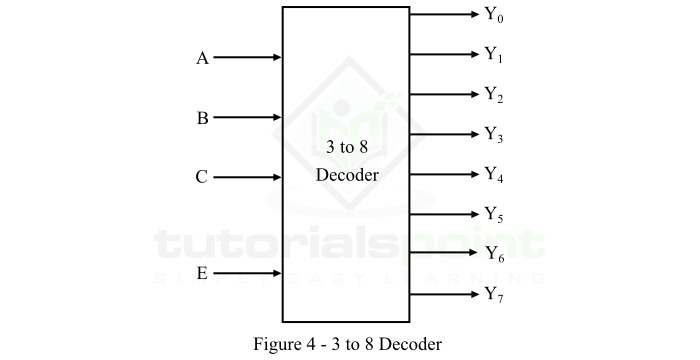
当使用使能输入E使该解码器启用时,则对于每种输入组合,其八个输出中的一个将被激活。可以使用下表给出的功能表来分析此3线到8线解码器的操作。
| 输入 | 输出 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E | A | B | C | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 |
| 0 | X | X | X | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
使用此功能表,我们可以导出每个输出的布尔表达式,如下所示:
$$\mathrm{Y_{0} \: = \: E \: \bar{A} \: \bar{B} \: \bar{C}}$$
$$\mathrm{Y_{1} \: = \: E \: \bar{A} \: \bar{B} \: C}$$
$$\mathrm{Y_{2} \: = \: E \: \bar{A} \: B \: \bar{C}}$$
$$\mathrm{Y_{3} \: = \: E \: \bar{A} \: B \: C}$$
$$\mathrm{Y_{4} \: = \: E \: A \: \bar{B} \: \bar{C}}$$
$$\mathrm{Y_{5} \: = \: E \: A \: \bar{B} \: C}$$
$$\mathrm{Y_{6} \: = \: E \: A \: B \: \bar{C}}$$
$$\mathrm{Y_{7} \: = \: E \: A \: B \: C}$$
我们可以看到,每个输出项都包含输入变量的乘积,因此可以使用与门来实现。因此,3到8解码器的逻辑电路图如图5所示。
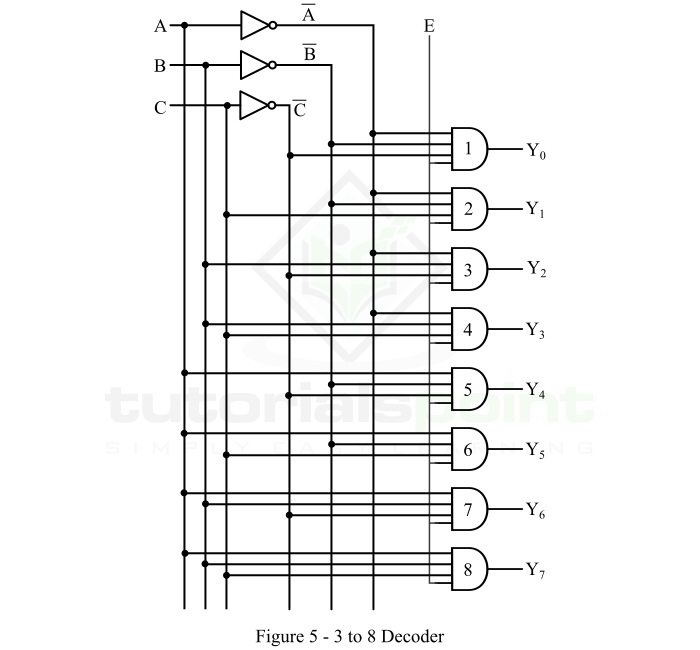
操作
3到8解码器逻辑电路的操作描述如下:
- 当使能输入(E)处于非活动状态,即设置为0时,任何与门都不会工作。
- 当使能输入(E)通过设置为1使其处于活动状态时,电路将按以下方式工作。
- 当A = 0,B = 0,且C = 0时,与门1被激活并产生输出Y0。
- 当A = 0,B = 0,且C = 1时,与门2被激活并产生输出Y1。
- 当A = 0,B = 1,且C = 0时,与门3被激活并产生输出Y2。
- 当A = 0,B = 1,且C = 1时,与门4被激活并产生输出Y3。
- 当A = 1,B = 0,且C = 0时,与门5被激活并产生输出Y4。
- 当A = 1,B = 0,且C = 1时,与门6被激活并产生输出Y5。
- 当A = 1,B = 1,且C = 0时,与门7被激活并产生输出Y6。
- 当A = 1,B = 1,且C = 1时,与门8被激活并产生输出Y7。
4到16解码器
4到16解码器是一种具有4条输入线和16(214)条输出线的解码器。4到16解码器的功能框图如图6所示。
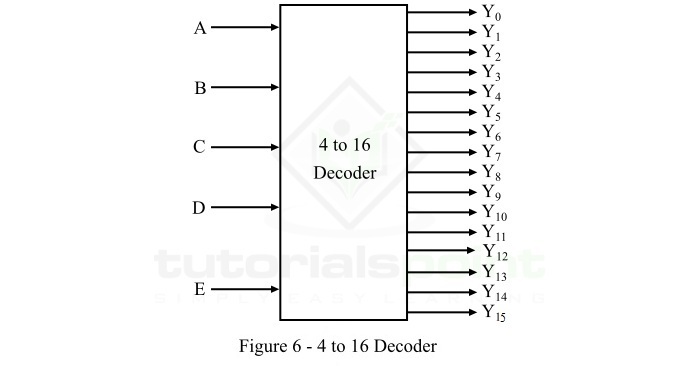
当使用使能输入E使该解码器启用时,则对于每种输入组合,其十六个输出中的一个将被激活。可以使用下表给出的功能表来分析此4线到16线解码器的操作。
| 输入 | 输出 | ||||
|---|---|---|---|---|---|
| E | A | B | C | D | |
| 0 | X | X | X | X | 0 |
| 1 | 0 | 0 | 0 | 0 | Y0 |
| 1 | 0 | 0 | 0 | 1 | Y1 |
| 1 | 0 | 0 | 1 | 0 | Y2 |
| 1 | 0 | 0 | 1 | 1 | Y3 |
| 1 | 0 | 1 | 0 | 0 | Y4 |
| 1 | 0 | 1 | 0 | 1 | Y5 |
| 1 | 0 | 1 | 1 | 0 | Y6 |
| 1 | 0 | 1 | 1 | 1 | Y7 |
| 1 | 1 | 0 | 0 | 0 | Y8 |
| 1 | 1 | 0 | 0 | 1 | Y9 |
| 1 | 1 | 0 | 1 | 0 | Y10 |
| 1 | 1 | 0 | 1 | 1 | Y11 |
| 1 | 1 | 1 | 0 | 0 | Y12 |
| 1 | 1 | 1 | 0 | 1 | Y13 |
| 1 | 1 | 1 | 1 | 0 | Y14 |
| 1 | 1 | 1 | 1 | 1 | Y15 |
从此功能表中,我们可以直接写出每个输出的布尔表达式,如下所示:
$$\mathrm{Y_{0} \: = \: E \: \bar{A} \: \bar{B} \: \bar{C} \: \bar{D}}$$
$$\mathrm{Y_{1} \: = \: E \: \bar{A} \: \bar{B} \: \bar{C} \: D}$$
$$Y_2 = E \bar{A} \bar{B} C \bar{D}$$
$$Y_3 = E \bar{A} \bar{B} C D$$
$$Y_4 = E \bar{A} B \bar{C} \bar{D}$$
$$Y_5 = E \bar{A} B \bar{C} D$$
$$Y_6 = E \bar{A} B C \bar{D}$$
$$Y_7 = E \bar{A} B C D$$
$$Y_8 = E A \bar{B} \bar{C} \bar{D}$$
$$Y_9 = E A \bar{B} \bar{C} D$$
$$Y_{10} = E A \bar{B} C \bar{D}$$
$$Y_{11} = E A \bar{B} C D$$
$$Y_{12} = E A B \bar{C} \bar{D}$$
$$Y_{13} = E A B \bar{C} D$$
$$Y_{14} = E A B C \bar{D}$$
$$Y_{15} = E A B C D$$
我们可以像实现2到4译码器和3到8译码器一样实现这些输出表达式。
现在,让我们讨论译码器的应用。
译码器的应用
译码器用于仅在特定输入代码组合出现时激活输出或一组输出的情况。下面列出了一些译码器的重要应用:
- 译码器用于代码转换。
- 译码器广泛应用于计算机的存储系统。
- 译码器也用于多路分解或数据分配。
- 译码器也用于需要非常短的传播延迟的数据路由应用。
- 译码器也可用于定时或排序目的。
- 译码器还用于在特定时间打开和关闭数字设备。
这就是关于译码器及其在数字电子系统中的应用。