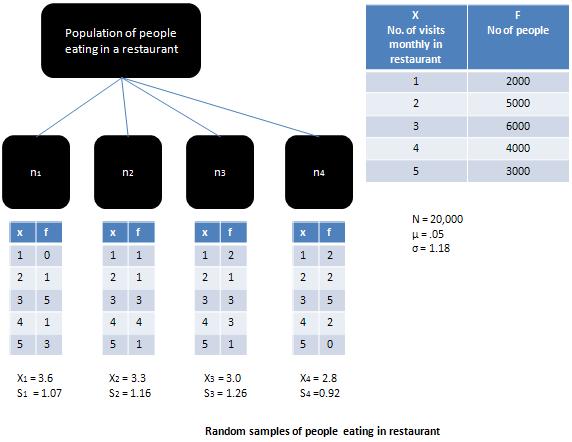
统计学 - 中心极限定理

如果样本所来自的总体是一个正态总体，那么**样本均值**将等于总体均值，并且**抽样分布**将是正态的。当总体更偏斜时，如图所示，那么**抽样分布**将趋向于更接近正态分布，前提是样本量足够大（即大于30）。

根据**中心极限定理**，对于样本量大于30的足够大的样本，**抽样分布**的形状将越来越像**正态分布**，而不管母体总体的形状如何。该定理解释了**总体分布**和**抽样分布**之间的关系。它强调了一个事实，即如果存在足够多的样本集，那么均值的**抽样分布**将接近**正态分布**。中心极限定理的重要性已被理查德·I·莱文用以下话概括：

中心极限定理的意义在于，它允许我们使用样本统计量来推断总体参数，而无需了解该总体频率分布的形状，除了我们从样本中获得的信息之外。