统计 - 逻辑回归

逻辑回归是一种统计方法，用于分析一个或多个自变量决定结果的数据集。结果是用二分变量（只有两个可能的结果）来衡量的。

公式

${\pi(x) = \frac{e^{\alpha + \beta x}}{1 + e^{\alpha + \beta x}}}$

其中 −

响应 - 特征的存在/不存在。
预测变量 - 每个案例观察到的数值变量
${\beta = 0 \Rightarrow }$ P（存在）在 x 的每个水平上都是相同的。
${\beta \gt 0 \Rightarrow }$ P（存在）随着 x 的增加而增加
${\beta \lt 0 \Rightarrow }$ P（存在）随着 x 的增加而减少。

示例

问题陈述

解决以下问题的逻辑回归：用于治疗偏头痛的瑞扎特里坦

响应 - 2 小时内完全缓解疼痛（是/否）。

预测变量 - 剂量 (mg)：安慰剂 (0)、2.5、5、10

剂量	患者数	缓解人数	缓解率
0	67	2	3.0
2.5	75	7	9.3
5	130	29	22.3
10	145	40	27.6

解决方案

已知 ${\alpha = -2.490} 和 ${\beta = .165}，我们有以下数据

$ {\pi(0) = \frac{e^{\alpha + \beta \times 0}}{1 + e^{\alpha + \beta \times 0}} \\[7pt] \, = \frac{e^{-2.490 + 0}}{1 + e^{-2.490}} \\[7pt] \\[7pt] \, = 0.03 \\[7pt] \pi(2.5) = \frac{e^{\alpha + \beta \times 2.5}}{1 + e^{\alpha + \beta \times 2.5}} \\[7pt] \, = \frac{e^{-2.490 + .165 \times 2.5}}{1 + e^{-2.490 + .165 \times 2.5}} \\[7pt] \, = 0.09 \\[7pt] \\[7pt] \pi(5) = \frac{e^{\alpha + \beta \times 5}}{1 + e^{\alpha + \beta \times 5}} \\[7pt] \, = \frac{e^{-2.490 + .165 \times 5}}{1 + e^{-2.490 + .165 \times 5}} \\[7pt] \, = 0.23 \\[7pt] \\[7pt] \pi(10) = \frac{e^{\alpha + \beta \times 10}}{1 + e^{\alpha + \beta \times 10}} \\[7pt] \, = \frac{e^{-2.490 + .165 \times 10}}{1 + e^{-2.490 + .165 \times 10}} \\[7pt] \, = 0.29 }$

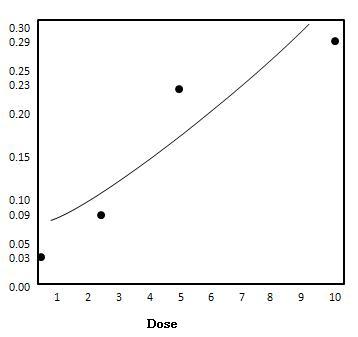
剂量(${x}$)	${\pi(x)}$
0	0.03
2.5	0.09
5	0.23
10	0.29

打印页面