统计学 - 维恩图

---

---

维恩图是一种直观地表示实体或对象组之间关系的方式。维恩图由圆圈组成，每个圆圈代表一个整体集合。维恩图可以有无限个圆圈，但通常情况下，两个或三个圆圈是比较理想的，否则图表会变得过于复杂。

绘制维恩图的步骤

考虑以下人群集合：

1. 板球运动员 - $C = \{ राम, श्याम, मोहन, रोहन, रमेश, सुरेश \}$

2. 曲棍球运动员 - $H = \{ रमेश, नरेश, महेश, लीला, सुनीता \}$

步骤1：画一个矩形，并将其标记为运动员。

步骤2：画两个圆圈，分别标记为板球和曲棍球。确保圆圈相互重叠。

步骤3：根据相关性在圆圈内写入姓名。共同的姓名应该落在公共区域内。

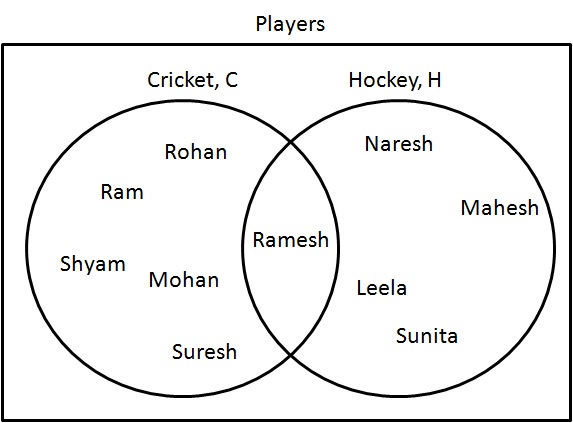
并集

并集 ($\cup$) 表示一个集合，其中包含所有类别中的项目，但不重复。

示例

问题陈述

绘制 $C \cup H$ 的维恩图。

解决方案

步骤1：确定既参加板球又参加曲棍球的运动员。绘制如下：

$C \cup H = \{ राम, श्याम, मोहन, रोहन, रमेश, सुरेश, नरेश, महेश, लीला, सुनीता \}$。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

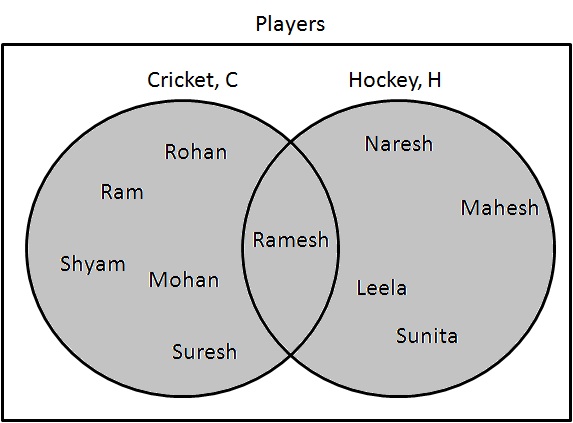
交集

交集 ($\cap$) 表示一个集合，其中包含两个类别中都存在的项目。

示例

问题陈述

绘制 $C \cap H$ 的维恩图。

解决方案

步骤1：确定既参加板球又参加曲棍球的运动员。绘制如下：

$C \cap H = \{ रमेश \}$。

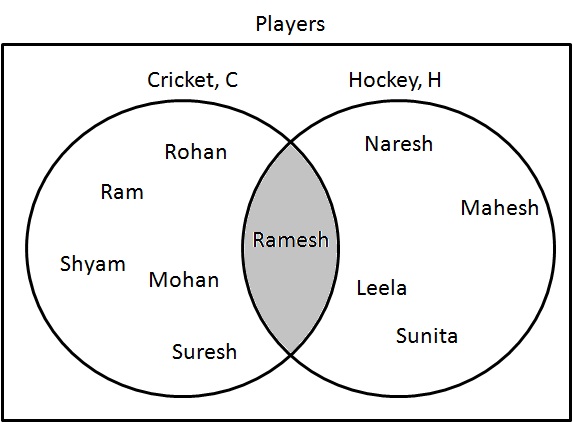
差集

差集 ($-$) 表示一个集合，其中只包含一个类别中存在的项目，而不包含另一个类别中的项目。

示例

问题陈述

绘制 $C - H$ 的维恩图。

解决方案

步骤1：确定只参加板球的运动员。绘制如下：

$C - H = \{ राम, श्याम, मोहन, रोहन, सुरेश \}$。